graniastoslup ada: W graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość 6 i tworzy z przekątną ściany bocznej,z którą ma wspólny wierzchołek,kąt o mierze równej α. oblicz objętość tego graniastosłupa.

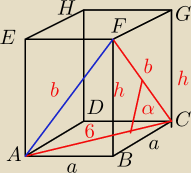
Janek191: Otrzymujemy Δ_ACF równoramienny, w którym

3
	= cos α
b

3 = b cos α

	3
b =
	cos α

−−−−−−−−−−−−−

	6
6 = a√2 ⇒ a =		= 3 √2
	√2

a = 3 √2 ⇒ a² = `18 −−−−−− Z tw. Pitagorasa mamy

	3		9
h2 + a2 = b2 ⇒ h2 = b2 − a2 = (		)2 − a2 =		− a2
	cos α		cos2α

więc h = √ ⁹_cos²α − 18 −−−−−−−−−−−−−− Objętość graniastosłupa V = P_p*h = a² *h = 18*√ ⁹_cos²α − 18 ==========================