pomocy.. jaa: Trapez równoramienny ABCD jest opisany na okręgu o promieniu 2√2cm. Wiedząc że przekątna tego trapezu ma długośc 2√17 cm, oblicz : a) długośc odcinka łączącego środki ramion trapezu b) pole trapezu c) długośc ramienia trapezu. Z góry dziękuje za pomoc.

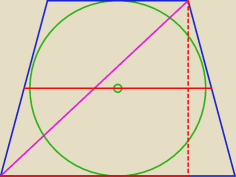
Tadeusz: ...dalej już wiesz −

jaaa: Nie wiem...:(

Tadeusz: ... nie rozumiesz, że odcinki czerwone są sobie równe ... Przekątną znasz (fioletowa) ... wysokość znasz (dwa promienie) ... Pitagorasa też znasz (w sumie fajny Facio) ... i licz −

jaaa: Policzyłam długość odcinka łączącego środki ramion i wysokość. Jak policzyć długości podstaw i ramienia? Poprowadzi ktoś? Bardzo proszę..

Eta:

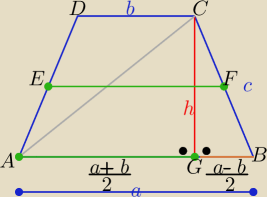
	a+b		a−b
h=2r=4√2 , |AC|=2√17 , |AG|=|EF|=		, |GB|=
	2		2

	a+b
z warunku wpisania okręgu w trapez : a+b=2c ⇒ c=
	2

z tw. Pitagorasa w trójkącie AGC : |AG|=√4*17−16*2 = 6 to: |EF|=6 , |CB|=|AD|=c= 6 |GB|=√6²−(4√2)²= ......... =2 rozwiąż ten układ: a−b=4 i a+b=12 .........

jaaa: Okej, już wszystko rozumiem. Dziekuje bardzo

Eta:

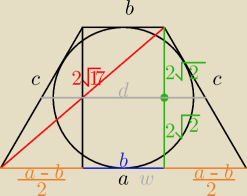
agulka: Jezeli czworokąt można opisać na okręgu, to suma jego przeciwległych boków jest równa. Z rysunku mamy: a+b=2c (1) Z tw. Pitagorasa (zykorzystaniem przekątnej trapezu):

	a−b
(2√17)2=(4√2)2+(		+b)2
	2

	a+b
68=32+(		)2
	2

	(a+b)2
36=		/*4
	4

144=(a+b)² a+b=12 Z równania (1) wiemy, że: a+b=2c 12=2c c=6 Z tw. Pitagorasa (z wykorzystaniem boku trapezu):

	a−b
c2=(4√2)2+(		)2
	2

	(a−b)2
36=32+
	4

	(a−b)2
4=		/*4
	4

16=(a−b)² a−b=4 Otrzymujemy układ równań:

⎧	a+b=12
⎩	a−b=4

Po obliczeniu mam:

⎧	a=8
⎩	b=4

Mając te dane obliczenie podpunktów nie powinno być trudne

jaaa: Tak, tak już rozumiem, poradziłam sobie. Dziekuję bardzo