geometria analityczna AlbertoKnox: Witam. Geometria analityczna. Napisz równanie okręgu przechodzącego przez punkt M (0,1) i stycznego do dwóch prostych o równaniach x+y−2=0 i x+y+3=0. Promień obliczyłem i mam jedno równanie z odległością od środka do punktu z dwoma niewiadomymi. Jak znaleźć drugie równanie? Chyba, że trzeba jakimś innym sposobem?

Tadeusz: Zauważyłeś pewnie, że podane proste są równoległe Wiesz zatem na jakiej prostej będą leżały środki szukanych okręgów − bo będą dwa −

AlbertoKnox: No tak bo środki będą z jednej i drugiej strony punktu. Ale nie wiem jak wyznaczyć tą prostą. Prosta równoległa y=x+b, ale skąd te b? Od r jakoś je uzależnić? I oczywiście już dziękuje za wszelką pomoc. A czyżby wyznaczyć prostą przez M i w jedną i drugą stronę r?

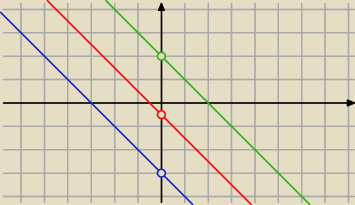
Tadeusz: masz proste: y=−x+2 y=−x−3 to jaki problem z wyznaczeniem b

AlbertoKnox: No fakt Sory, że zamotałem, pisałem o równoległej a myślałem o prostopadłej. Dzięki teraz to już chyba zrobię.