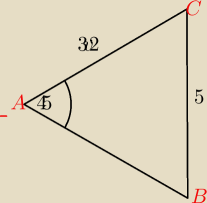
oblicz pole trójkąta wexe: AC = 3√2 BC = 5 kąt BAC = 45* a) oblicz pole trójkąta ABC b)promień okręgu wpisanego, wynik zapisz w postaci a+b√c. a,b ∊ W, c ∊ N.

PW: Stosując twierdzenie cosinusów obliczymy długość AB. Mając |AB| i |AC| oraz kąt BAC obliczymy pole.

wexe: doszedłem do c² = −6√2*c − 7√2 Co dalej można z tym zrobić ?

wexe: Mógłby mi ktoś obliczyć bok AB ?

PW: Nie wiem skąd wziąłeś takie równanie, chyba fantazja zadziałała, a nie twierdzenie cosinusów. W twierdzeniu tym muszą wystąpić bok i kąt leżący naprzeciwko, a więc |BC|² = |AC|² + |AB|² − 2|AC| |AB|cos∡CAB 5² = (3√2)² + |AB|² − 2(3√2)|AB|os45°. Po oznaczeniu dla krótkości zapisu |AB| = x > 0 otrzymamy równanie:

	√2
25 = 18 + x2 − 2(3√2)x		, x > 0.
	2