okręgi
xxx:
proszę o jakąś podpowiedź, pomoc, cokolwiek, bo ja nie wiem jak to udowodnić
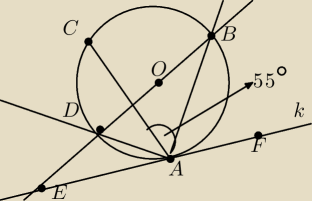
Prosta k jest styczna w punkcie A do okręgu o środku w puncie O. Z punktu A poprowadzono dwie
cięciwy AB i AC, które utworzyły kąt 55°. Półprosta BO→ przecina okrąg w punkcie D i prostą k
w punkcie E (zobacz rysunek obok). Wykaż, że jeśli półprosta AB→ jest dwusieczną kąta FAC, to
półprosta AD→ jest dwusieczną kąta EAC.
na razie ustaliłam tyle że:
kąt BAD = 90
kąt DAC = 90 − 55 = 35
ale nie wiem co z tym dalej zrobić
 proszę o jakąś podpowiedź, pomoc, cokolwiek, bo ja nie wiem jak to udowodnić
Prosta k jest styczna w punkcie A do okręgu o środku w puncie O. Z punktu A poprowadzono dwie
cięciwy AB i AC, które utworzyły kąt 55°. Półprosta BO→ przecina okrąg w punkcie D i prostą k
w punkcie E (zobacz rysunek obok). Wykaż, że jeśli półprosta AB→ jest dwusieczną kąta FAC, to
półprosta AD→ jest dwusieczną kąta EAC.
na razie ustaliłam tyle że:
kąt BAD = 90
kąt DAC = 90 − 55 = 35
ale nie wiem co z tym dalej zrobić
proszę o jakąś podpowiedź, pomoc, cokolwiek, bo ja nie wiem jak to udowodnić
Prosta k jest styczna w punkcie A do okręgu o środku w puncie O. Z punktu A poprowadzono dwie
cięciwy AB i AC, które utworzyły kąt 55°. Półprosta BO→ przecina okrąg w punkcie D i prostą k
w punkcie E (zobacz rysunek obok). Wykaż, że jeśli półprosta AB→ jest dwusieczną kąta FAC, to
półprosta AD→ jest dwusieczną kąta EAC.
na razie ustaliłam tyle że:
kąt BAD = 90
kąt DAC = 90 − 55 = 35
ale nie wiem co z tym dalej zrobić


