Nlity
Radek:
| | 29 | | 13 | |
Do okręgów o równaniach x2+7x+y2+5y+ |
| =0 i x2−x+y−3y− |
| poprowadzono wspólną |
| | 2 | | 2 | |
styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
Wyznaczyć równania okręgów i co mam robić dalej ?
26 mar 17:36
Radek: ?
26 mar 18:02
Mila:
Po 20, teraz za chwilę będę zajęta.
Napisz równiania okręgów w postaci kanonicznej , aby znac środki i promienie.
26 mar 18:04
Radek:
Dobrze poczekam, będę robił inne zadania.
26 mar 18:06
Piotr 10: Wskazówka; Poszukaj trójkątów podobnych
26 mar 18:06
Radek: czemu z podobieństwa ?
26 mar 20:39
Tadeusz:
... bo znasz promienie ...policzysz odległość środków ... no i znasz Taleska −

26 mar 20:57
Radek:
Dziękuję spróbuje tym Talesem

26 mar 20:59
Mila:
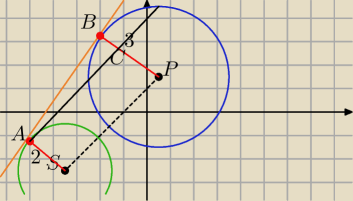
I przypadek
No i gdzie te równania?
Kreślę AC||PS
Oblicz PS,
Potem AB z ΔABC z tw. Pitagorasa
Dokończysz?
II przypadek zrobisz? Czy narysować?
26 mar 21:01
Radek:
Robiłem jednokładność. Proszę o rysunek. Tylko dziwne, że mam wykorzystywać Taelsa skoro to
geometria analityczna. ?
26 mar 21:12
Mila:
Dokończyłeś I przypadek?
Geometria to i Pitagoras i Tales .
26 mar 21:18
Radek:
W pierwszym mam √31 ?
26 mar 21:21
Mila:
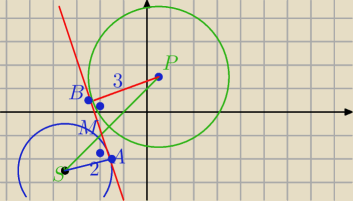
|MS|+|MP|=|PS|
ΔPBM∼ΔSAM
Dalej sam.
26 mar 21:25
Radek:
AB2=√7
Mogę jeszcze kilka zadań z którymi mam kłopot ?
26 mar 21:30
Mila:
Pisz.
26 mar 21:34
Radek:
Punkty B = (0,10) i O = (0,0) są wierzchołkami trójkąta prostokątnego OAB , w którym |∡OAB |
| | 1 | |
= 9 0∘ . Przyprostokątna OA zawiera się w prostej o równaniu y = |
| x . Oblicz |
| | 2 | |
współrzędne punktu A i długość przyprostokątnej OA
Robię z tego
(0−0)
2+(0−10)
2=(x−0)
2+(0,5x−0)
2+(x−0)
2+(0,5x−10)
2
x
2−2x=0
x(x−2)=0
x=0 lub x=2
coś chyba nie tak ?
26 mar 21:37
Mila:
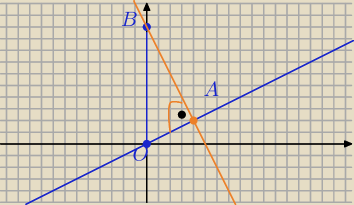
źle rozwiązałeś równanie, trzeba dać założenie x≠0
x=4
A=(4,2)
II sposób
Prostopadła do k
y=−2x+10
oblicz x, a potem y
26 mar 21:50
Radek:
Założenie ? Gdzie mam błąd w równaniu ?
26 mar 21:53
Mila:
| | 1 | | 1 | |
100=x2+ |
| x2+x2+ |
| x2−10x+100 |
| | 4 | | 4 | |
2,5x
2−10x=0
2,5x(x−4)=0 ⇔
x=0 nie odpowiada założeniom, bo nie powstanie Δ.
lub x=4
26 mar 22:42
Radek:
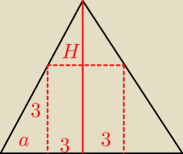
Dziękuję a teraz mam problem z bryłą
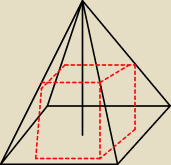
W ostrosłupie prawidłowym czworokątnym wpisano sześcian o krawędzi 6 w taki sposób, że cztery
wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe 4 do jego podstawy. Ściana
boczna jest nachylona do płaszczyzny podstawy pod kątem 30
0 Oblicz pole powierzchni tego
ostrosłupa Oblicz pole tego ostrosłupa
H=3a+6
I potem jeśli mam
2H=x
x=(6a+12)
i teraz pitagorasa
H
2+U({a}{2})
2=(6a+12)
2 ?
26 mar 22:56
Tadeusz:
... sprawdź tą pierwszą proporcję −

26 mar 23:10
Mila:
Dlaczego nie skorzystasz z tg 30 aby obliczyc połowę krawedzi podstawy.
Poza tym wysokość sześcianu to 6.
26 mar 23:14
Radek:
Wpadłem na taki pomysł
26 mar 23:15
Mila:
Nie widzę w tym sensu. ( MOże jest, ale nie widzę)
Czy rysować?
26 mar 23:17
Radek:
Ale czemu nie ma w tym sensu ?
26 mar 23:18
Radek:
18+6a=3H−18
H=2a+12
x=2H
x=4a+24
| | a | |
(4a+24)2=( |
| )2+(2a+12)2 |
| | 2 | |
z tego mogę wyznaczyć więc chyba ma to jakiś sens.
26 mar 23:26
Radek:
26 mar 23:31
Mila:
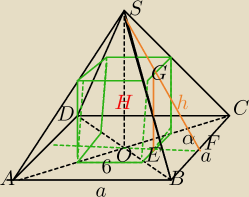
W ΔGEF:
W ΔSOF:
Z tw. Pitagorasa , albo sinusa, albo cosinusa alfa oblicz h
I to będzie wszystko co potrzebne.
26 mar 23:46
Mila:
Dobranoc

26 mar 23:49
Radek:
Ale czemu mój pomysł jest nie dobry. ? delta w moim wychodzi
√Δ=160 ale potem dwa ujemne
rozwiązania ?
| | 6 ? | |
A Czemu w Pani rozwiązaniu tgα= |
| |
| | a−2/3 | |
| | H−6 | |
tgα= |
| chyba tak powinno być ? |
| | | |
26 mar 23:51
Mila:
Radku popatrz na oznaczenia.
|EG|=6
a− bok kwadratu ( krawędzi podstawy).
26 mar 23:55
Radek:
Dobrze, dziękuję ale jeszcze będę szukał błędu u siebie bo też powinno z tego wyjść
26 mar 23:58
Radek: nie mogę sie dopatrzeć co robię źle ?

27 mar 17:53
Mila:
Korzystasz z podobieństwa Δ. Napisz jakich to odpowiem. Co oznaczyłeś literą a?
Z moich proporcji wychodzi dobrze.
27 mar 17:56
Radek:
a−krawędź podstawy
H−wysokość ostrosłupa
27 mar 18:04
Mila:
Radek odcinek 3+a nie leży w podstawie.
27 mar 18:07
Radek:
Już wiem gdzie robię błąd. Dziękuję.
27 mar 18:14
Mila:
Dobrze.
27 mar 18:29
Radek:
A pomoże jeszcze Pani z bryłami i anlityczną ?
27 mar 18:29
Mila:
Tak. Policzyłeś zgodnie z odpowiedzią?
27 mar 18:34
Radek:
Poprawiłem swój sposób i też wyszło, Pani sposobem wyszło poprawnie ale ja zawsze też chcę
rozwiązać swoim sposobem tym na co ja wpadłem

27 mar 18:37
Radek:
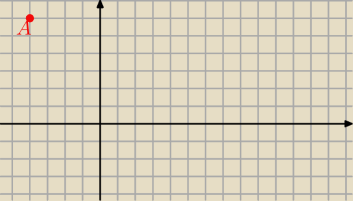
Wyznacz równanie takiej prostej przechodzącej przez punkt A (− 4,6) , która wraz z osiami
układu współrzędnych ogranicza trójkąt o polu równym 2
?
27 mar 18:42
Mila:
y=ax+b
6=−4a+b, b=4a+6
y=ax+4a+6
oblicz miejsce zerowe
Możesz rozważyć dla x
0>0 i b>0, a potem skorzystać z symetri wzgledem punktu O(0,0)
27 mar 18:56
Radek:
Skąd ta prosta ?
27 mar 18:57
Mila:
Przeciez masz polecenie, aby narysować prostą.
27 mar 18:59
Radek:
No ok a dalej nie wiem co mam robić ?
27 mar 19:00
zawodus: Obliczyć to co podała ci Mila

27 mar 19:04
Radek: ale jak z tej postaci mam obliczyć MZ
y=ax+4a+b
0=ax+4a+b
ax=−4a−b
27 mar 19:07
Mila:
ax+4a+6=0 z tego oblicz x
27 mar 19:07
Radek:
ax+4a+6=0
ax=−4a−6=0
27 mar 19:19
zawodus: I liczysz pole.
27 mar 19:25
Radek:
Xo znam a b to niewiadoma ?
27 mar 19:33
zawodus: Najlepiej zrób przykład na konkretach i potem do tego się odnieś.
27 mar 19:43
Mila: b=4a+6
27 mar 19:49
Radek:
Ale jak wyznaczyć b z tego ?
27 mar 19:51
Mila:
Podstawiasz do wzoru 18:56 na pole Δ i otrzymujesz równanie z niewiadomą a.
27 mar 19:53
Radek:
Ale chodzi jak Pani wyznaczyła b z tej prostej ?
27 mar 19:57
zawodus: A jak masz prostą y=2x+4 to ile wynosi b?
27 mar 20:01
Radek:
b=4
27 mar 20:05
zawodus: To tutaj masz jakie b?
27 mar 20:07
Radek:
4a+6
Ale jeszcze pytanie skąd w tym wzorze |b| i |x0| i czemu w module ?
27 mar 20:09
Mila:
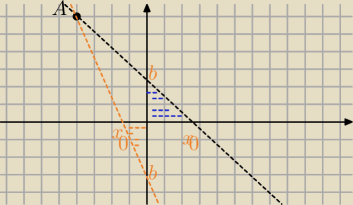
W module , bo pole jest nieujemne.
y=ax+b
(0,b) punkt przecięcia osi OY
Rozważam, że takie mogą być przypadki.
27 mar 20:27
Radek:
Z równaniem to sobie poradzę tylko chciałem wiedzieć skąd to x0 i b we wzorze
27 mar 20:29
Mila:
Jasne już?
27 mar 20:51
Radek:
Ale co oznacza x
o i b w tym wzorze
| | 1 | |
P= |
| *wysokość razy podstawa |
| | 2 | |
27 mar 20:53
Mila:
długości przyprostokątnych.
27 mar 20:56
Radek:
Dziękuję teraz muszę się zabrać za te bryły

27 mar 20:58
Radek:
Wysokość prawidłowego ostrosłupa sześciokątnego ma długość H , a krawędź podstawy ma długość a
. Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek
ostrosłupa
Chcę tylko rysunek.
27 mar 21:39
Mila:
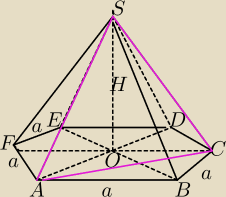
Np.
ΔACS
27 mar 22:23
27 mar 22:31
Mila: AC dobrze.
SC, żle obliczone i nie trzeba tego liczyć.
Masz obliczyć wysokość ΔACS
27 mar 23:08
Radek:
Ale OC to nie jest połowa dłużej przkątnej 3a ?
27 mar 23:22
Mila:
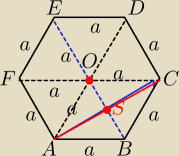
|OC|=a
|FC|=2a
27 mar 23:28
Radek:
Dziękuję.
27 mar 23:30
Mila: 
27 mar 23:48
Radek:
Wyszedł poprawny wynik już teraz.
27 mar 23:49
Mila:
Cieszę się. DObranoc

27 mar 23:50
Radek:
Jutro postaram się zrobić więcej zadań. Dobranoc.
27 mar 23:51
Radek:
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego
wysokość oraz przez dwie krawędzie boczne
Mogę prosić o rysunek ?
28 mar 21:17
Radek:
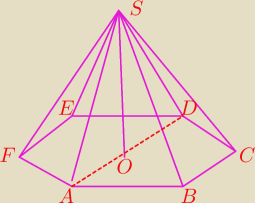
ADS ?
28 mar 21:26
zawodus: tak?
28 mar 21:38
Radek:
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego
wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi
6
√3. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
28 mar 22:06
bezendu: ok
28 mar 22:25


 I przypadek
No i gdzie te równania?
I przypadek
No i gdzie te równania?
 |MS|+|MP|=|PS|
ΔPBM∼ΔSAM
Dalej sam.
|MS|+|MP|=|PS|
ΔPBM∼ΔSAM
Dalej sam.
 źle rozwiązałeś równanie, trzeba dać założenie x≠0
x=4
A=(4,2)
II sposób
źle rozwiązałeś równanie, trzeba dać założenie x≠0
x=4
A=(4,2)
II sposób
 Dziękuję a teraz mam problem z bryłą
W ostrosłupie prawidłowym czworokątnym wpisano sześcian o krawędzi 6 w taki sposób, że cztery
wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe 4 do jego podstawy. Ściana
boczna jest nachylona do płaszczyzny podstawy pod kątem 300 Oblicz pole powierzchni tego
ostrosłupa Oblicz pole tego ostrosłupa
Dziękuję a teraz mam problem z bryłą
W ostrosłupie prawidłowym czworokątnym wpisano sześcian o krawędzi 6 w taki sposób, że cztery
wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe 4 do jego podstawy. Ściana
boczna jest nachylona do płaszczyzny podstawy pod kątem 300 Oblicz pole powierzchni tego
ostrosłupa Oblicz pole tego ostrosłupa


 W ΔGEF:
W ΔGEF:



 Wyznacz równanie takiej prostej przechodzącej przez punkt A (− 4,6) , która wraz z osiami
układu współrzędnych ogranicza trójkąt o polu równym 2
?
Wyznacz równanie takiej prostej przechodzącej przez punkt A (− 4,6) , która wraz z osiami
układu współrzędnych ogranicza trójkąt o polu równym 2
?

 W module , bo pole jest nieujemne.
y=ax+b
(0,b) punkt przecięcia osi OY
Rozważam, że takie mogą być przypadki.
W module , bo pole jest nieujemne.
y=ax+b
(0,b) punkt przecięcia osi OY
Rozważam, że takie mogą być przypadki.

 Np.
ΔACS
Np.
ΔACS
 |OC|=a
|OC|=a


 ADS ?
ADS ?