Oblicz długość odcinka AD.
mnichuu:
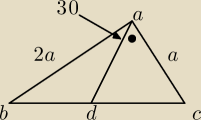
W trójkącie ABC środkowa AD jest prostopadła do boku AC. Kąt BAC ma miarę 120 oraz
|AB|=2|AC|=2a. Oblicz długość odcinka AD.
|AC|=a
<CAB=120
|AB|=2a
<CAD=90
|AD|=?
Jak się za to zabrać? Jakaś wskazówka?
26 mar 17:28
pigor: ..., np. tak : niech
|AD|=x= ? , to z ΔCAD : |CD|=
√x2+a2= |BD|
to z tw. cosinusów i ΔABD : BD
2= AD
2+x
2−2|AD|x*cos30
o ⇔
⇔ x
2+a
2= 4a
2+x
2−4ax*
12√3 ⇔ −3a
2= −2ax
√3 ⇔
⇔ 2x
√3= 3 /*
√3 ⇔ 6x= 3
√3 /:6 ⇒ x=
|AD|= 12√3 . ...

26 mar 17:45
mnichuu: up
26 mar 17:45
mnichuu: wybacz, nie zauważyłem, już ogarniam

26 mar 17:45
mnichuu: do tego momentu wszystko rozumiem .. −3a2=−2ax√3 ..
Po jednej stronie masz a2 a po drugiej a, co takiego robisz, że zanikają po obu stronach?
26 mar 17:52
pigor: ... , oj, przepraszam zgubiłem literkę a
od tego miejsca : −3a2= −2ax√3 ⇔ 3a= 2xp{3] itp. skończ
..................
a jak to ci się nie podoba zrób "po swojemu",
też z tw. cosinusów, ale z ΔABC .
26 mar 17:57
mnichuu: muszę powiedzieć, że łatwy i przyjemny sposób

dzięki wielkie
26 mar 18:01
 W trójkącie ABC środkowa AD jest prostopadła do boku AC. Kąt BAC ma miarę 120 oraz
|AB|=2|AC|=2a. Oblicz długość odcinka AD.
|AC|=a
<CAB=120
|AB|=2a
<CAD=90
|AD|=?
Jak się za to zabrać? Jakaś wskazówka?
W trójkącie ABC środkowa AD jest prostopadła do boku AC. Kąt BAC ma miarę 120 oraz
|AB|=2|AC|=2a. Oblicz długość odcinka AD.
|AC|=a
<CAB=120
|AB|=2a
<CAD=90
|AD|=?
Jak się za to zabrać? Jakaś wskazówka?


 dzięki wielkie
dzięki wielkie