trygonometria diana: Dla jakich wartości parametru a istnieje rozwiązanie równania: cos²x=a²−3a+2/a+1 proszę o rozwiązane krok po kroku..

Mila:

	a2−3a+2
cos2x=
	a+1

a+1≠0⇔a≠−1 a²−3a+2=0 Δ=9−4*2=1

	3−1		3+1
a=		lub a=
	2		2

a=1 lub a=2 0≤cos²x≤1 w takim razie :

	a2−3a+2
0≤		≤1⇔
	a+1

a2−3a+2		a2−3a+2
	≥0 i		≤1 i a≠−1⇔
a+1		a+1

(a−1)*(a−2)		a2−3a+2
	≥0 i		−1≤0 i a≠−1⇔
a+1		a+1

	a2−3a+2−a−1
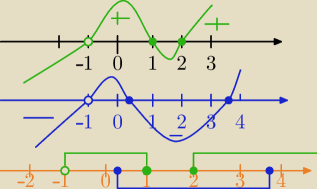
(a−1)*(a−2)(a+1)≥0 i		≤0 ⇔
	a+1

	a2−4a+1
x∊(−1,1>U<2,∞) i		≤0 [ Δ=12, a1=2−√3 lub a2=2+√3]
	(a+1)

[x∊(−1,1>U<2,∞) ] i [x∊(−∞,−1)U <2−√3, 2+√3>] część wspólna x∊<2−√3,1>U <2,2+√3>

diana: dziękuję bardzo. mam jeszcze pytanie: skąd się wzieło '0≤cos2x≤1'?

Mila: Z definicji cosinusa i tego, że a²≥0 dla a∊R