przedziały piotrrrr: Wyznacz przedział w ktorym funkcja f(x)=−1/2(x−2)²+1 jest malejąca oraz zbiór wartości funkcji.

J: Licz Δ i miejsca zerowe.

mirek: gdzie jestes janko

Mila:

	−1
f(x)=		(x−2)2+1 postać kanoniczna trójmianu kwadratowego.
	2

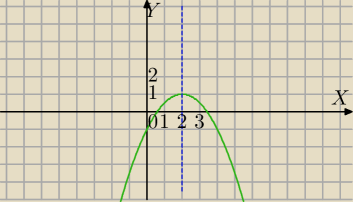
(2,1) −współrzędne wierzchołka paraboli skierowanej w dół. dla x≥2 funkcja malejąca 1 − najwieksza wartość f(x) Zw=<−∞,1>

pigor: ..., ponieważ masz daną postać kanoniczną funkcji kwadratowej f, o "delcie" i miejscach zerowych ... zapomnij, bo wszystko masz we wzorze kanonicznym f , czyli tu : f(x)= −¹₂(x−2)²+1 i a= −1<0, więć parabola ma ramiona do dołu, to f jest malejąca ⇔ x >2 ⇔ x∊(2;+∞), a zbiór wartości to y≤1 ⇔ y∊(−∞;1] i tyle. ...

Janko: Gdy a czyli w tym przypadku −1/2 jest ujemna to funkcja ma ramiona do dołu, a jeśli jest dodatnia to do góry i teraz ta postać Mirek jest kanoniczna a to oznacza, że wyraża się wzorem : y = a(x−p)² + q czyli wyznaczamy z tego wierzchołek (punkt przegięcia z obszaru gdzie jest rosnąca na malejącą lub odwrotnie z malejącej na rosnącą) i teraz robimy przedziały dla malejącej : od (p;+∞), czyli od (2;+∞), a zbiór wartości to wszystko co poniżej (dla "a" ujemnego a powyżej dla innego zadania w którym "a" byłoby dodatnie) wierzchołka łącznie z nim, czyli: zbiór wartości : (−∞;1]