Wyznacz dziedzinę funkcji walt:

	2−x−x2
Wyznacz dziedzinę funkcji f(x)=log2+x:3−x
	(x+2)3

	2+x
W podstawie logarytmu mamy
	3−x

Ad.1 a>0

2+x
	>0
3−x

(2+x)(3−x)>0 x=−2 x=3 x∊(−2,3) Ad.2 a≠0

2+x
	≠1
3−x

2+x−3+x
	≠0
3−x

2x−1
	≠0
3−x

2x−1≠0

	1
x≠
	2

Ad.3 tutaj mam mały problem, zrobiłem to tak: 2−x−x²>0 x²+x−2<0 (x+2)(x−1)<0 x∊(−2,1) ale mam obawy czy tego nie powinienem zrobić czasem tak: wyliczyłem Δ, i mam : (x+2)(x−1) w liczniku, czyli:

(x+2)(x−1)
	=U{x+1}{(x+2)2= x+1 , wyrażenie jest dodatnie gdy x>−1
(x+2)3

Proszę o pomoc

J: Co jest liczbą logarytmowaną ?

J: Co do podstawy logarytmu a, to warunki są takie: a > 0 a ≠ 1

walt: Nie rozumiem pytania, a poza tym przecież zastosowałem a>0 i a≠0 dla podstawy.

J: Napisałem Ci wyraźnie, podstawa a musi spełniać warunki: a > 0 i a ≠ 1

J: Natomiast liczba logarytmowana b musi być większa od 0

walt:

2+x		2+x
	>0 i		≠0
3−x		3−x

Wyliczyłem to przecież

	1
x∊(−2,3) x≠
	2

coś tutaj zrobiłem źle

J: Tłumaczę Ci jak dziecku: a > 0 i a ≠ 1. Dla podstawy logarytmu nie trzeba warunku a = 0, przecież a > 0 wyklucza już a = 0. Nie ogarniasz tego ?

walt: co do ostatniego Ad.3

2−x−x2
	>0
(x+2)3

(x+2)(x−1)
	>0
(x+2)3

x−1
	>0
(x+2)2

(x−1)(x+2)²>0 x=1 x∊(1,oo)

J: Poczytaj to :https://matematykaszkolna.pl/strona/217.html , może Ci rozjaśni.

J: Ad 3. (2 − x − x²)(x + 2)³ > 0

J: Ad 3. OK: x > 1

walt: Zacznę od początku. Podstawa logarytmu musi być dodatnia i nie może być równa 1, na początek sprawdzę kiedy jest równa 1.

2+x
	=1
3−x

2+x−3+x
	=0
3−x

2x−1=0

	1
x=
	x

	1
Zatem x≠		. Teraz sprawdzę kiedy podstawa jest dodatnia.
	2

2+x
	>0
3−x

(2+x)(3−x)>0 x∊(−2,3)

	2−x−x2
Teraz rozkładam licznik wyrażenia
	(x+2)3

(x+2)(x−1)

	(x+2)(x−1)
Zatem		>0
	(x+2)3

(x−1)(x+2)²>0 x=1 brak pierwiastków x∊(1,oo) Czy mój tok rozumowania jest zły? Tak zawsze rozwiązywałem te zadania i w tym momencie nie widzę żadnego błędu

walt:

	1		1
chochlik się wkradł, zamiast x=		ma być x=
	x		2

walt: hm?

walt: up

nocny marek: −x²−x+2≠(x+2)(x−1)

walt: a, nie przeniosłem minusa. a=−1 −x²−x+2=0 Δ_x=1+8 √Δ_x=3

	1−3
x1=		=1
	−2

	1+3
x2=		=−2
	−2

−x²−x+2=0=−(x+2)(x−1)

walt: ad.3 x∊(−oo,−1) Nocny Marku, czyli pozostałe rzeczy są dobrze obliczone? Mogę przejść do wyznaczenia dziedziny?

nocny marek: masz rozwiązać nierówność

W(x)
	>0 ⇔ W(x)*Q(x)>0 i Q(x)≠0
Q(x)

nocny marek: (2−x−x²)(x+2)³ ma być jakie >0 <0?

walt: >0

nocny marek: To oś liczbowa m zerowe i wykres a nastepnie odpowiedź.

walt: miejsca zerowe: x₁=−2 − pierwiastek 4−krotny x₂=1 x∊(−oo,−2) U (−2,1) Zgadza się?

walt: Gdybyś mi mógł jeszcze wytłumaczyć jedną rzecz, mianowicie: Mam to Ad.3 gdzie wyliczam W(x)/Q(x) >0 a co z założeniami a>0 i a≠1 które wyliczyłem wcześniej. Byłbym ogromnie wdzięczny.

nocny marek: Zapisz zadanie , ponieważ nie rozumię o co Tobie chodzi

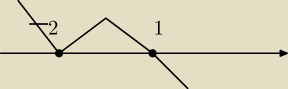
nocny marek: zgadza

walt: napiszę całe zadanie jak to widzę od początku, wytłumacz mi proszę co jest potrzebne co nie, co jest źle a co jest nie dobrze i dlaczego tak jest.

	2−x−x2
Wyznacz dziedzinę funkcji f(x)=log2+x/3−x
	(x+2)3

	2+x
W podstawie logarytmu jest
	x−3

Podstawa logarytmu musi być dodatnia i nie może być równa 1, na początek sprawdzę kiedy jest równa 1.

2+x
	=1
3−x

2+x−3+x
	=0
3−x

2x−1=0

	1
x=
	2

	1
Zatem x≠
	2

Teraz sprawdzę kiedy podstawa jest dodatnia.

2+x
	>0
3−x

(2+x)(3−x)>0 x∊(−2,3)

2−x−x2
	>0
(x+2)3

−(x+2)⁴(x−1)>0 wyznaczam miejsce zerowe: x₁=−2 −pierwiastek 4−krotny x₂=1 − 1−krotny x∊(−oo,−2) U (−2,1) Teraz ustalam dziedzinę spośród tego co obliczyłem. Czekam cierpliwie na wytłumaczenie

nocny marek:

	1
x≠		zapomniałeś
	2

nocny marek:

	2+x
Jedna uwaga raz podstawę log piszesz		a innym w mianowniku (x−3)
	3−x

walt:

	1
nie zapomniałem. Jest zapisane "zatem x≠
	2

Ma być 3−x, wkradł się chochlik

nocny marek: ale w D nie uwzględniłeś.

walt: Nie ustaliłem jej w tamtym poście jeszcze.

	1
Czyli Df=x∊(−oo,−2) U (−2,1) / {		}
	2

walt: a co się dzieje z tym wyrażeniem: x∊(−2,3) ? Tej trójki nie uwzględniamy w dziedzinie

walt: proszę o cierpliwość do mej osoby

nocny marek: Musisz wziąsć wspólną część! Nanieś sobie na oś liczbową i będziesz przekonany

walt: "część wspólna", dzięki, wszystko już wiem