Rozwiąż równanie + podaj załorzenia
Grzes:
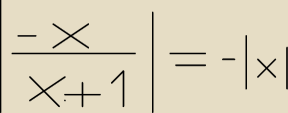
26 mar 13:14
wredulus_pospolitus:
bez rozwiązywania ... pomyśl
lewa strona będzie ZAWSZE ≥ 0 (dlaczego

)
prawa strona będzie ZAWSZE ≤ 0 (dlaczego

)
w takim razie kiedy możliwa jest równość

26 mar 13:15
Grzes: x= 0
26 mar 13:25
pigor: ...oj te Twoje zało
żenia przez rz strasznie rażą

26 mar 13:28
Grzes: heheh.. nawet nie zauważyłem...

26 mar 13:31
pigor: .., ale z tym x=0 masz rację

tylko może bys to jakoś ładnie "ubrał" matematycznie , co

26 mar 13:34
26 mar 13:44
Grzes: no i tu mam problem jak to napisać matematycznie..

26 mar 13:44
Grzes: | | ⎧ | x gdy x≥0 | |
| |x| = | ⎨ | |
|
| | ⎩ | −x gdy x<0 | |
26 mar 13:45
koleżka: równianie będzie spełnione jeśli jedna strona będzie równa zero:
wiec
|x|≥ 0 to jest w własnościach wart bezwzgl
−|x|≤0 bo jest minus więc zmiana znaku
czyli x∊(−∞,0>
zero jest uwzględniane więc podstawiając zero do 2 równań mamy spełnioną równość.
26 mar 13:50
koleżka: Szanowny Panie PIGOR
dobrze mówie ?
26 mar 13:51
pigor: ... no niestety szanowny
koleżko nie, bo np. podstaw
sobie jakąś liczbę ujemną np. x= −2 i co zobaczysz

26 mar 14:05
pigor: ..., to , że tylko x=0 spełnia daną nierówność widać ...,
a jak to "mądrze" rozpisać ? może np. tak :z własności wartości
bezwzględnej między innymi |−x|=|−1||x|= |x|,a wtedy
| | −x | | |x| | |
| |
| |= −|x| i x−1≠0 ⇔ |
| = −|x| /*|x−1| i x≠1 ⇔ |
| | x−1 | | |x−1| | |
⇔ |x|= −|x| |x−1| i x≠1 ⇒ |x|+|x| |x−1|= 0 ⇔ |x| (1+|x−1|)= 0 ⇔
⇔ |x|= 0 v 1+|x−1|= 0 ⇔ x= 0 v |x−1|= −1 ⇔ x=0 v x∊∅ ⇔
⇔
x=0 ⇔
x∊{0} − szukane rozwiązanie . ...

26 mar 14:18
koleżka: nooo Twój sposób mi się podoba

ja się sugerowałem częścią wspólną przedziałów i częścią wspólną było 0

26 mar 14:38
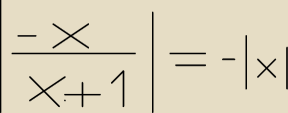
 )
prawa strona będzie ZAWSZE ≤ 0 (dlaczego
)
prawa strona będzie ZAWSZE ≤ 0 (dlaczego )
w takim razie kiedy możliwa jest równość
)
w takim razie kiedy możliwa jest równość 


 tylko może bys to jakoś ładnie "ubrał" matematycznie , co
tylko może bys to jakoś ładnie "ubrał" matematycznie , co 



 ja się sugerowałem częścią wspólną przedziałów i częścią wspólną było 0
ja się sugerowałem częścią wspólną przedziałów i częścią wspólną było 0 