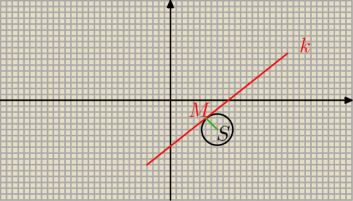
geometria analityczna tyu: proszę o sprawdzenie zadania "znajdź równanie okręgu o środku w punkcie S(3, −2) stycznego do prostej o równaniu k: 3x−4y−12=0",

	3
czyli mam tutaj znaleźć r tego okręgu, więc k: y=		x−3
	4

1/ szukam prostej (np n)przechodzącej przez punkt S(3, −2), która jest prostopadła do prostej k

	4
a1a2=−1 a2=−
	3

	4
y=−		x + 2
	3

2/ szukam miejsca przecięcia się prostych n oraz k, czyli szukam punktu M

3		4
	x−3=−		x + 2 x=2,4 y=−1,2
4		3

3/ liczę odległość pomiędzy M i S IMSI = √ (2,4−3)² + (−1,2 − 2)² = √ 0,36 + 10,24 ≠ 1, gdyż 1 to właściwa odpowiedź 1=r

Maslanek: Sprawdź punkt (3). Tam jest błąd

tyu: ale gdzie, bo ja go nie widzę. sprawdziłem pkt 3. wszystko wydaje się dobrze być policzone

Maslanek: Odległości punktów są nieprawdziwe

tyu: nie rozumiem, co oznacza "nieprawdziwe"

tyu:

Maslanek: Przekłamane, nieprawidłowe, źle policzone.

tyu: M (x_m= 2,4; y_m= −1,2) S(x_s= 3; y_s= −2) IMSI = √ (x_s − x_m)² + (y_s − y_m)² = √ (3−2,4)² + (−2−1,2)² = √ 0,6² + (−3,2)² = √ 0,36+ 10,24 = √ 10,6 gdzie jest błąd

pigor: ..., tu masz błąd y_s−y_m=−2−1,2=−3,2 ... , a tak powinno być : y_s−y_m= −2−(−1,2)= = −2+1,2= −0,8

tyu: dzięki