Logarytmy 3 Qmi: Logarytmy 3 Wyznacz zbór rozwiązania nierówności

	1
log/div>		(−x2+4x+5) >= −3
	2

	1
Zał x>		<−− Poprawne założenie?
	2

	1		1
log/div>		(−x2+4x+5) >= log/div>		8
	2		2

różnowartościowość −x²+4x+5 >= 8 −x²+4x−3 >= 0 Delta = 16 − 12 = 4 pierw. = 2 x₁ = 3 x₂ = 1

	1
Zał x>
	2

x należy do <1,3> To wszystko?

Piotr: jaka jest podstawa logarytmu ? dziedzina : −x² + 4x + 5 > 0

Piotr: zreszta zobacz tu https://matematykaszkolna.pl/strona/252.html

Qmi:

	1
Podstawa to
	2

Czyli Df = (−1,5) Czyli należy

	1
a co z tym
	2

Piotr: odwrociles znak nierownosci gdy opuszczales logarytmy ? uprzedzam, ze liczyc mi sie nie chce

	1
z		nic. taka jest po prostu podstawa logarytmu, nie ma tam niewiadomej przeciez.
	2

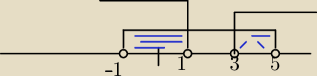
Qmi: Czyli rozwiązanie to x należy (−1, 1) u (3,5)

Qmi: Po odwróceniu tak mi wychodzi, kompletnie zapomniałem o tym że się odwraca

Piotr: masz ≥ chyba to czemu wszedzie nawiasy okragle ?

Qmi: Sorki. Zapomniałem Czyli tylko nawiasy ostre i będzie git?

Qmi: 2gie podobne zadanie.

	1
log/div>		(x2 + x) >= −1
	2

	1		1
log/div>		(x2 + x) >= log/div>		2
	2		2

x²+x <= 2 x²+x − 2 <= 0 Delta = 9 , pierw z delty = 3 x₁ = −1 x₂ = 2 Rozw: x należy <−1 , 2 > Df = x² + x > 0 x(x+1) > 0 x > −1

Piotr: nie wszedzie ostre w tym poprzednim (przypominam, ze tego nie licze ) to drugie : dziwnie wszystko piszesz. Dziedzina : x² + x > 0 i masz źle PS ja spadam ogladac mecz