ciągi czarnoksiężnik.OZ: Suma ilu poczatkowych wyrazow ciagu (a_n) okreslonego wzorem a_n=2n²−17n−42, jest najmniejsza? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− obliczyłem miejsca zerowe tej funkcji i wyszło −2 i 10,5 oraz wierzchołek paraboli x=4,25 i myślałem że najmniejsza wartość to ta w wierzchołku i będzie suma 4 początkowych, a ma być 10. Jak ma do tego dojść?

wredulus_pospolitus: 'na chłopski rozum' miejsca zerowe paraboli to −2 i 10,5 więc wartość dla n=1 jest ujemna dla n=2 także dla n=3 także itd. aż w końcu dla n=10 ujemna dla n=11 dodatnia a więc S₁ < 0 ale S₂ będzie jeszcze mniejsze od S₁ S₃ mniejsze od S₂ itd. S₁₀ mniejsze od S₉ ale już S₁₁ będzie większe od S₁₀ bo pierwszy raz w sumie zajdzie się DODATNI element

J: a₁ = 2 − 17 − 42 = −57

	−57 +an
0 =		*n
	2

J: Przeczytałem... jest równa zero, nie było postu

czarnoksiężnik.OZ: dzięki już wiem o co chodzi

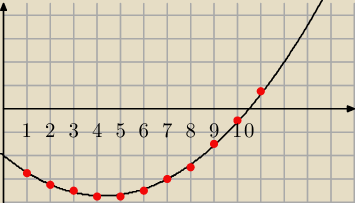
Trivial: Jeszcze interpretacja graficzna. Widać, że do a₁₁ suma zacznie się powiększać.

Trivial: od a₁₁...

czarnoksiężnik.OZ: no właśnie jak sobie narysuje to wydaje mi się że najmniejsza jest w wierzchołku...

wredulus_pospolitus: najmniejszy WYRAZ ale nie SUMA

czarnoksiężnik.OZ: dlatego muszę sobie po kolei rozpisać

Trivial: Sumujemy S₁ = a₁ S₂ = a₁ + a₂ S₃ = a₁ + a₂ + a₃ ... S₁₀ = a₁ + a₂ + ... + a₁₀ Wyrazy a₁,...,a₁₀ są ujemne. Dodając a₁₁ powiększymy wartość sumy.

czarnoksiężnik.OZ: no tak czym więcej ujemnych tym mniejsza liczba. a jeszcze np. jakby było odwrotnie znaczy parabola ramionami w dół to 10 byłby największy?