Wykaż, że |MK|=|ML|
Truck:
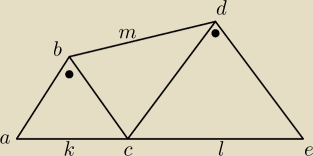
Trójkąty ABC i CDE są równoramienne i prostokątne. Punkty A,C i E leżą na jednej prostej, a
punkty K,L,M są środkami odcinków AC,CE i BD. Wykaż, że |MK|=|ML|
Mógłby ktoś pomóc mi z tym zadaniem ?

25 mar 12:06
Truck: Ja to widzę mniej więcej tak:
(ΔABC ~ ΔDEF) |AB|=|BC| |CD|=|DE| jeśli |BM|=|MD| to:
|MK|=|ML|
25 mar 12:09
Truck: 
25 mar 12:37
Eta:
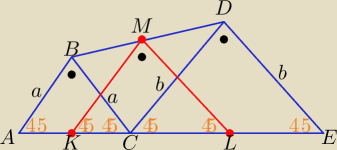 1 sposób
1 sposób
zauważ trapezy : ABCD i BCDE bo AB ∥CD i BC∥DE
Odcinki KM i ML są środkowymi tych trapezów
| | a+b | | a+b | |
zatem |KM|= |
| i |ML|= |
| ⇒ |KM|=|ML| |
| | 2 | | 2 | |
c.n.w
2 sposób
Odcinki KL∥AB ⇒ |<CKM|=45
o i ML∥BC ⇒|<CLM|=45
o
zatem trójkąt KML jest równoramienny i prostokątny o ramionach |KM|=|ML|
c.n.w
25 mar 12:40
Truck: To jest takie banalne a czasami tak ciężko na to wpaść.

Wszystko jest trudne zanim staje się łatwe
25 mar 12:58
Truck: dzięki Eta,

dla Ciebie

25 mar 12:59
Eta:

25 mar 12:59
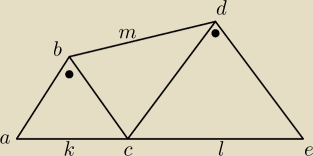 Trójkąty ABC i CDE są równoramienne i prostokątne. Punkty A,C i E leżą na jednej prostej, a
punkty K,L,M są środkami odcinków AC,CE i BD. Wykaż, że |MK|=|ML|
Mógłby ktoś pomóc mi z tym zadaniem ?
Trójkąty ABC i CDE są równoramienne i prostokątne. Punkty A,C i E leżą na jednej prostej, a
punkty K,L,M są środkami odcinków AC,CE i BD. Wykaż, że |MK|=|ML|
Mógłby ktoś pomóc mi z tym zadaniem ? 

 1 sposób
zauważ trapezy : ABCD i BCDE bo AB ∥CD i BC∥DE
Odcinki KM i ML są środkowymi tych trapezów
1 sposób
zauważ trapezy : ABCD i BCDE bo AB ∥CD i BC∥DE
Odcinki KM i ML są środkowymi tych trapezów
 Wszystko jest trudne zanim staje się łatwe
Wszystko jest trudne zanim staje się łatwe
 dla Ciebie
dla Ciebie 
