AS:
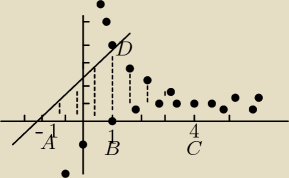
Szukane pole to obszar
ΔABD w przedziale <−1,1>
pod krzywą y = 4/x w <1,4> pomniejszony o obszar
pod krzywą y =
√x − 1 w <1,4>
Wyznaczam granice całkowania dla y = 4/x
y = 2*x + 2 i y = 4/x rozwiązanie tego układu daje wynik x1 = −2 i x2 = 1
Pole powierzchni trójkąta ABD
1 1
A = |(2*x + 2)dx = x
2 + 2*x | = (1
2 + 2*1) − ((−1)
2 + 2*(−1)) = 3 − (−1) = 4
−1 −1
Wyznaczam granice całkowania dla y =
√x − 1
4/x =
√x − 1 rozwiązanie tego układu daje wynik x = 4
Pole obszaru pod krzywą y = 4/x w przedziale <1,4>
4 4
B = | (4/x)dx = 4*ln(x) | = 4*ln(4) − 4*ln(1) = 4*ln(4) − 4*0 = 4*ln(4)
1 1
Pole obszaru pod krzywą y =
√x − 1 w przedziale <1,4>
4 4 4
C = |(
√x − 1)dx = |(x
1/2 − 1)dx = (x
3/2)/(3/2) − x | = (2/3)*8−4)−((2/3)*1−1) = 5/3
1 1 1
Ostatecznie szukane pole wynosi
S = A + B − C = 4 + 4*ln(4) − 5/3 = 7/3 + 4*ln(4) ≈ 7.8785 j
2
 Szukane pole to obszar
ΔABD w przedziale <−1,1>
pod krzywą y = 4/x w <1,4> pomniejszony o obszar
pod krzywą y = √x − 1 w <1,4>
Wyznaczam granice całkowania dla y = 4/x
y = 2*x + 2 i y = 4/x rozwiązanie tego układu daje wynik x1 = −2 i x2 = 1
Pole powierzchni trójkąta ABD
1 1
A = |(2*x + 2)dx = x2 + 2*x | = (12 + 2*1) − ((−1)2 + 2*(−1)) = 3 − (−1) = 4
−1 −1
Wyznaczam granice całkowania dla y = √x − 1
4/x = √x − 1 rozwiązanie tego układu daje wynik x = 4
Pole obszaru pod krzywą y = 4/x w przedziale <1,4>
4 4
B = | (4/x)dx = 4*ln(x) | = 4*ln(4) − 4*ln(1) = 4*ln(4) − 4*0 = 4*ln(4)
1 1
Pole obszaru pod krzywą y = √x − 1 w przedziale <1,4>
4 4 4
C = |(√x − 1)dx = |(x1/2 − 1)dx = (x3/2)/(3/2) − x | = (2/3)*8−4)−((2/3)*1−1) = 5/3
1 1 1
Ostatecznie szukane pole wynosi
S = A + B − C = 4 + 4*ln(4) − 5/3 = 7/3 + 4*ln(4) ≈ 7.8785 j2
Szukane pole to obszar
ΔABD w przedziale <−1,1>
pod krzywą y = 4/x w <1,4> pomniejszony o obszar
pod krzywą y = √x − 1 w <1,4>
Wyznaczam granice całkowania dla y = 4/x
y = 2*x + 2 i y = 4/x rozwiązanie tego układu daje wynik x1 = −2 i x2 = 1
Pole powierzchni trójkąta ABD
1 1
A = |(2*x + 2)dx = x2 + 2*x | = (12 + 2*1) − ((−1)2 + 2*(−1)) = 3 − (−1) = 4
−1 −1
Wyznaczam granice całkowania dla y = √x − 1
4/x = √x − 1 rozwiązanie tego układu daje wynik x = 4
Pole obszaru pod krzywą y = 4/x w przedziale <1,4>
4 4
B = | (4/x)dx = 4*ln(x) | = 4*ln(4) − 4*ln(1) = 4*ln(4) − 4*0 = 4*ln(4)
1 1
Pole obszaru pod krzywą y = √x − 1 w przedziale <1,4>
4 4 4
C = |(√x − 1)dx = |(x1/2 − 1)dx = (x3/2)/(3/2) − x | = (2/3)*8−4)−((2/3)*1−1) = 5/3
1 1 1
Ostatecznie szukane pole wynosi
S = A + B − C = 4 + 4*ln(4) − 5/3 = 7/3 + 4*ln(4) ≈ 7.8785 j2