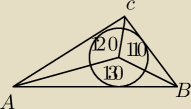
Planimetris problem_matematyczny: Podrzuciłby ktoś pomysł ? Dany jest trójkąt ABC jak na rysunku, gdzie O oznacza środek okręgu wpisanego w ten trójkąt. Wyznacz miary kątów wewnętrznych tego trójkąta.

Hajtowy: Nawet tam na rysunku O nie widzę

problem_matematyczny: to ten środek koła, ale mi się nie zmieściło i by miary kątów zakryło

Mila: Środek okręgu wpisanego w Δ leży na przecięciu dwusiecznych kątów wewnętrznych trójkąta Kolejno mamy:

1		1		1		1
	α+		β+130=180⇔		α+		β=50
2		2		2		2

1		1		1		1
	β+		γ+110=180⇔		β+		γ=70
2		2		2		2

1		1		1		1
	γ+		α+120=180⇔		γ+		α=60
2		2		2		2

dokończ.

problem_matematyczny: ooo rzeczywiście wyszło, dziękuję

pigor: ..., niech ∡A=2α, ∡B=2β, ∡C=2γ , to α+β= 180−130= 50^o γ−β= 10^o β+γ= 180−110= 70^o −/stronami 3−1 ⇒ γ+β= 70^o /± stronami 1+2 ⇒ γ+α= 180−120= 60^o γ+α= 60^o ⇒ 2γ=80^o=∡C i 2β=60^o=∡B i 2α=2(60^o−γ)= 120−2γ=40^o=∡A . ...

problem_matematyczny: dzięki, dzięki ^^