planimetria bezendu: W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza 2a+a+c=14 3a+c=14 c=14−3a I teraz funkcja kwadratowa ? a²+2a²+c² a²+4a²+(14−3a)² o to chodzi ?

...: dawno nie widziałem czegoś głupszego ...

bezendu: Właśnie z tego coś wychodzi.. Aha fajnie. Ale teraz wyjdź...

Saizou : no raczej tak

bezendu: @... jak widać Twój komentarz zbędny, skoro nie umiesz to się nie wypowiadaj nie potrzebnie.

Saizou : Twój bezendu też, i mój też który teraz napisałem

bezendu: A tego nie trzeba napisać za pomocą funkcji f(x)=.. ?

Saizou : można i chyba trzeba, ja bym napisał za pomoc ą funkcji f(a)=.... i pamiętaj o dziedzinie!

bezendu: Dziedzina D=R ?

...: "I teraz funkcja kwadratowa ?" Wszystko co napisałeś/napisałaś po tym zadziwia mnie i nie mogę pojąć jak przebrnąłeś przez I klasę

bezendu: Widzisz jakoś się udało. Ale nie wiem co Ty tutaj teraz robisz ? Skoro nie pomagasz to czemu się udzielasz ?

Saizou : a no dziedzina to nie liczby rzeczywiste kiedy można zbudować trójkąt ?

...: ... pomagać można komuś kto cokolwiek umie ... tobie można pisać tylko gotowce (których i tak nie ogarniasz). Wiem co mówię bo jestem tu nie od dziś ...

bezendu: A jeszcze do @.. funkcję kwadratową miałem w drugiej klasie więc chyba coś Ci nie wyszło:( a+b>c

bezendu: @... ale niczym nie zabłysnąłeś do Tej pory więc Kończ już.

Saizou : tylko ?

bezendu: Nie tylko b+c>a a+c>b

Saizou : no i git, za bark dziedziny obcinają punkty

bezendu: Ok dziękuję

bezendu:

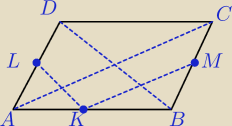
	1
Dany jest romb ABCD o boku długości 1, w którym kąt BAD jest ostry i sin ∡BAD=		. Na
	7

bokach AB ,AD i BC wybrano odpowiednio punkty K ,L i M w ten sposób, że odcinki KL i KM są równoległe do przekątnych rombu. Oblicz pole czworokąta CDLM .

Mila: W zadaniu 1, masz błąd w zapisie. Boki Δ: a,2a,c a+2a+c=14⇔c=14−3a Suma kwadratów boków: a,2a,14−3a F(a)=a²+(2a)²+(14−3a)² Po obliczeniu boków, sprawdź, czy boki mogą mieć obliczone długości ( to znaczy, czy można z nich zbudować Δ)

bezendu: Dziękuję już zrobiłem. A w tym drugim ?

Mila: CDLM jest trapezem o podstawach CM i DL. Wysokość jest równa wysokości rombu, to oblicz z porównania pola. Dalej sam, teraz idę na kolację.

bezendu:

	1
Zrobiłem z podobieństwa i wyszło		?
	14

Mila:

bezendu: Dobrze to teraz może być stożek ?

bezendu: Połówkę koła o promieniu 12 zwinięto w stożek. Oblicz objętość i kąt rozwarcia tego stożka jeżeli długość łuku tej połówki koła jest obwodem podstawy, a jej promień jest tworzącą stożka Tylko potrzebny rysunek bo dopiero zaczynam

Mila: α− kat rozwarcia dł.łuku=obwód podstawy stożka Promień wycinka = tworząca stożka

bezendu: Dziękuję.

bezendu: 12=2πr 6=πr

	6
r=
	π

o takie coś chodzi w tym zadaniu.

Mila:

	1
łuk=		*2π*R=π*12 długość półokręgu o promieniu R=12
	2

12π=2π*r r=6 l=12 teraz kąt rozwarcia ...

bezendu: ze wzoru na długość łuku mam co ?

Mila: Długość półokręgu. (zielone na wycinku koła)

bezendu:

	1
Dlatego		tak ?
	2

bezendu: kąt rozwarcia 60⁰

Mila: Tak, bo 2r=12, mamy w przekroju Δ równoboczny.

bezendu: Ok, dziękuję. Jutro będzie więcej zadań

Eta: