Janek191:
Pole Δ
P = 8*r + x*r + 6*r = ( 14 + x)*r = (14 + x)*4 = 56 + 4 x
| | 6 + 8 + 8 + x + x + 6 | |
p = |
| = 14 + x |
| | 2 | |
więc
p − a = 6
p − b = 8
p − c = x
więc z wzoru Herona
P =
√ p(( p − a)*( p − b)*(p − c) =
√(14 + x)*6*8*x =
√ 672 x + 48 x2
czyli
√ 672 x + 48 x2 = 56 + 4 x ; podnosimy obustronnie do kwadratu
672 x + 48 x
2 = 3 136 + 448 x + 16 x
2
32 x
2 + 224 x − 3 136 = 0 / : 32
x
2 + 7 x − 98 = 0
Δ = 49 − 4*1*( −98) = 441
√Δ = 21
==================
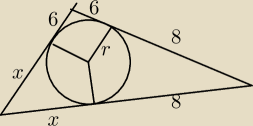 W trójkąt wpisano okrąg o promieniu 4. Punkt styczności dzieli jeden z boków na odcinki
długości 6 i 8. Obliczyć x.
W trójkąt wpisano okrąg o promieniu 4. Punkt styczności dzieli jeden z boków na odcinki
długości 6 i 8. Obliczyć x.