dowód kasia: wykaz, że jeżeli trójkąt jest równoramienny, to odcinki dwusiecznych kątów przy podstawie, zawarte w tym trójkącie, mają taką samą długość. Narysowałam trójkąt ale jaki mam napisać dowód? Proszę o pomoc

wredulus_pospolitus: 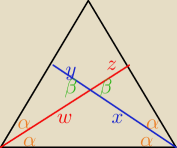α ponieważ mamy dwusieczną równoramiennego 'mały trójkąt' (o ramionach w i x) jest równoramienny ... w takim razie w=x (logiczne) β sobie równie na mocy odpowiedniego twierdzenia o kątach przy prostych przeciętych skoro dwa 'boczne' trójkąty mają dwa takie same kąty i jeden bok (pomiędzy tymi kątami) to są to trójkąty przystające ... w takim razie y=z c.n.w.

PW: Trójkąt równoramienny ma oś symetrii k − prostą zawierającą wierzchołek i środek podstawy. W symetrii osiowej obrazem kąta jest kąt przystający (o tej samej mierze), a więc obrazem jednej z dwusiecznych jest druga (kąty utworzone przez dwusieczne i półproste zawierające podstawę są przystające). Wobec tego odcinki dwusiecznych zawarte w trójkącie też są przystające (mają równe długości). Dobrze by było po narysowaniu wprowadzić oznaczenia literowe i powyższy dowód napisać używając tych oznaczeń.

PW: O, niepotrzebnie się trudziłem. Uszanowania, wredulusie.

pigor: ..., lub jeśli D,E punkty przecięcia dwusiecznych ramion AC=BC odpowiednio, kąt wierzchołkowy ACB wspólny i równe miary kątów CAE=CBD, zatem ΔAEC ≡ ΔBDC przystające (cecha kbk), więc |AE| = |BE| c.n.w. . ...

kasia: jejku co to znaczy c.n.w. a ten dowód to jest wszystko to co napisane

wredulus_pospolitus: c.n.w. −−− Co Należało Wykazać to co napisałem to jest 'objaśnienie' ... Ty musisz to "ładnie ubrać w zdania" w końcu nie możesz napisać, np.: "... skoro dwa 'boczne' trójkąty mają ... " Rusz głową przyszła kobieto ... rusz głową.