:) anita22:

	1		|x−1|		|x+2|
f(x)=		x+		+		narysuj wykres funkcji
	2		x−1		x+2

mietek: znasz definicję modułu?

anita22: znam, próbowałam to zrobić ale wyszły mi jakieś cuda i chciałabym się upewnić czy mam dobrze

PW: Cuda polegają na tym, że

	|u|		|u|
		= 1 lub		= −1,
	u		u

w zależności od znaku u. Należy więc rozpatrywać przedziały (−∞,−2), [2,1) i [1,∞), na których ułamki mają wartość 1 lub −1.

PW: O, o, oczywiście przedziały otwarte, bo x=−2 i x=1 nie należą do dziedziny!

PW: To już napiszę jeszcze raz: − Należy rozpatrywać przedziały (−∞,−2), (−2, 1) i (1,∞). Na pierwszym oba ułamki mają wartość −1, na drugim pierwszy ułamek ma wartość −1 i drugi 1, na trzecim przedziale oba ułamki mają wartość 1.

anita22: ....

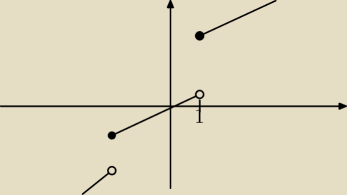
anita22: wyszło mi coś takiego, mógłby mi ktoś powiedzieć czy tak ma być oczywiście jednostki nie są tutaj idealne

anita22:

PW: Te kółeczka muszą być puste wszystkie (to co pisałem o 9:14 − liczby −2 i 1 nie należą do dziedziny). Na kolejnych przedziałach otwartych będą to wykresy funkcji:

	1
y =		x − 2,
	2

	1
y =		x,
	2

	1
y =		x +2.
	2