Nierówność
Domel: Jak określić przedział x−ów dla poniższej nierówności:
x − √2x2 − 4 ≥ 0
24 mar 00:53
ICSP: 1. Dziedzina
2. Przerzuć pierwiastek na drugą stronę
3. Dla x ≥ 0 podnieś obustronnie do kwadratu.
4. Rozwiąż nierówność kwadratową.
24 mar 00:58
Domel: Dziedzina → x∊(−oo; −√2> ∧ <√2; +oo)
x − √2x2 − 4 ≥ 0
dla x ≥ 0
x ≥ √2x2 − 4 /2
x2 ≥ 2x2 − 4
−x2 + 4 ≥ 0 => x∊<0; 2>
Uwzględniając dziedzinę → x∊<√2; 2>
a co z x < 0
24 mar 01:57
ICSP: Podstaw do nierówności :
x ≥ √2x2 − 4
dowolną liczbę ujemną za x i zobacz co się stanie.
24 mar 01:59
Domel: Nooooooooo − późno już

trzeba kłaść się spać bo mój mózg już chrapie

24 mar 02:02
24 mar 02:04
Janek191:
x −
√ 2x2 − 4 ≥ 0
2x
2 − 4 ≥ 0
x
2 ≥ 2
x ≤ −
√2 lub x ≥
√2
D = ( −
∞ ; −
√2 > ∪ <
√2 ; +
∞ )
−−−−−−−−−−−−−−−−−−−−−−−
x ≥
√2 x2 − 4
Dla x ≥
√2 podnosimy obustronnie do kwadratu:
x
2 ≥ 2 x
2 − 4
0 ≥ x
2 − 4
x
2 − 4 ≤ 0 ⇔ x ∊ < − 2; 2>
zatem x ∊ <
√2 ; 2 >
=================
24 mar 06:48
Janek191:
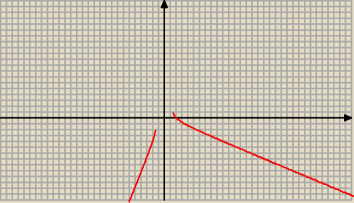
Wykres funkcji
y = x −
√2 x2 − 4
y ≥ 0 ⇔ x ∊ <
√2 ; 2 >
24 mar 06:51
Domel: No w porządku
2. Dla przypadku
x −
√2x2 − 4 ≤ 0
Dziedzina jw. czyli x∊(−oo; −
√2> ∧ <
√2; +oo)
x ≤
√2x2 − 4
dla
x ≥ √2 podnoszę do kw.
x
2 ≤ 2x
2 − 4
x
2 −4 ≥ 0 => x ≤ −2 ∧ x ≥ 2
A z warunkiem
x ≥ √2 mamy tylko x ≥ 2
a co dla
x ≤ −√2 

No i są jeszcze przypadki:
3. x +
√2x2 − 4 ≥ 0
4. x +
√2x2 − 4 ≤ 0
Kurde, żeby tłumaczyć innej osobie to sam muszę to w końcu zrozumieć.
25 mar 19:28
ICSP: x ≥ √2x2 − 4
dla x ≤ − √2 mamy:
Liczba ujemna ≥ liczba dodatnia
Skąd od razu masz sprzeczność.
Pozostałe 3 nierówności robisz w sposób identyczny. Ogólnie jeżeli masz nierówność z
pierwiastkiem
25 mar 21:15
Wazyl: Domel po pierwsze zrób założenie:
x−
√coś≥0 ⇒ x ≥
√coś.
√coś≥0

x≥0
25 mar 21:16
Domel: No w punkcie 2 powinno być x≥2 i x≤−√2 − jak dojść do drugiego rozwiązania?
25 mar 21:20
Domel: A w punktach 3 − 4 − to pierwiastek przenoszę na drugą stronę czy liczbę? I podnoszę potem do
kwadratu? (dla jakich założeń?)
25 mar 21:23
ICSP: Pomyśleć
x ≤ √2x2 − 4
dla x ≤ − √2 lewa strona jest ujemna, a prawa jest dodatnia. Wnioski zostawiam tobie
25 mar 21:24
pigor: ..., np. tak :
x−√2x2−4 ≥0 i 2x
2−4 ≥0 ⇔
⇔
√2x2−4≤ x /
2 i x>0 (dla x≤0 sprzeczność, dlaczego ?) i x
2 ≥2 ⇔
⇔ 2x
2−4≤ x
2 i x>0 i x
2≥2 ⇔ 2≤ x
2≤ 4 ⇔ x>0 i
√2≤ |x| ≤ 2 ⇔
⇔
√2 ≤ x ≤ 2 ⇔
x∊ [√2; 2] − szukany
zbiór rozwiązań . ...

25 mar 21:28
Domel: pigor pierwszy przypadek mam zrobiony − walczę z punktami 2, 3 i 4
ICSP czyli no... sorki faktycznie − logika − a ja szukałem równań lub nierówności

25 mar 21:35
ICSP: 2 też już masz zrobiony

25 mar 21:43
Domel:
3.
x + √2x2 − 4 ≥ 0 => x∊(−oo; −√2> ∧ <√2; +oo)
x ≥ − √2x2 − 4
x ≥ √2 => x ≥ − √2x2 − 4
x ≤ −√2 => x ≥ − √2x2 − 4 /2
x2 ≥ 2x2 − 4
x2 − 4 ≤ 0 => x∊<−2; −√2> − no i to jest chyba (a raczej na pewno) BYK
25 mar 21:49
ICSP: Podnosząc do kwadratu dwie liczby ujemne zmieniasz znak nierówności.
25 mar 21:53
Mila:
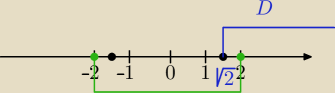
1) D:
2x
2−4≥0⇔x≤−
√2 lub x≥
√2
2)
x≥
√2x2−4 ponieważ
√2x2−4 ≥0 to x>0 ( x=0 nie należy do dziedziny)
D: x∊<
√2,
∞)
Możemy podnieść obie trony nierówności do kwadratu
x
2≥2x
2−4⇔
x
2−4≤0⇔x∊<−2,2> i x∊D⇔x∊<
√2,2>
25 mar 22:04
pigor: ...., po co tracić czas na te twoje przypadki

warto napisać daną nierówność w takiej postaci równoważnej,
aby z definicji pierwiastka st. 2 wykluczyć x< 0 (zaś x=0 przez podstawienie
nie sprawdza tej nierówności) i nie mów, że ja rozpatrzyłem tylko 1−szy
przypadek ; moje rozwiązanie jest kompletne i tyle.

25 mar 22:07
ICSP: pigor ale to są IV różne nierówności

25 mar 22:08
Domel: Ok pigor − źle się wyraziłem − nie pierwszy przypadek tylko rozwiązałeś pierwszą (z
czterech) nierówność.
Nierówność druga jest klarowna (dzięki ICSP)
Ale nierówności trzecią i czwartą (dotyczy mojego postu z 19:28) − no jeszcze walczę.
Ponieważ nie jestem niestety α i Ω to szukam kogoś kto wyjaśni te − być może dla ciebie
trywialne − dylematy
25 mar 22:20
pigor: ... widzę, że nikt nie pochylił się uważnie nad 1) moim
rozwiązaniem i 2) moim wyjaśnieniem w 2−gim poście; może
więc przypomnę, że dana nierówność
x−
√2x2−4 ≥0 ⇔
√2x2−4≤ x dla x≤ 0 nie ma sensu bo od
kiedy to pierwiastek kwadratowy może być ujemny

(
√a=
b ≥ 0 )
25 mar 22:30
pigor: ...ależ ja grzecznie, chcę tylko uprzytomnić, że szkoda tracić
czas na tak bezproduktywną robotę, i jeszcze może brać za to kasę

25 mar 22:39
Mila:
22:04 rozpisałam to , co podał w pigułce pigor.
25 mar 22:40
Domel: pigor − nie "biorę kaski" za uczenie syna mojej partnerki ale nie chcę też walić mu bzdur
do głowy (jeżeli sam nie mam pewności jak to działa) − no a jeżeli tak cię boli "pochylanie
się" i lubisz uszczypliwości − to polecę ci dobrego ortopedę
ICSP mam nadzieję, że w końcu zajarzyłem
a więc 2−gi warunek w 3 nierówności to:
x ≤ −√2 => x ≥ −
√2x2 − 4 /
2
x
2 ≤ 2x
2 − 4
x2 − 4 ≥ 0 => x ≤ −2 ∧ x ≥ 2
ponieważ
x ≤ −√2 to x ≤ −2
No to dla 3−ciej nierówności x ≥
√2 ∧ x ≤ −2
4.
x +
√2x2 − 4 ≤ 0 − dziedzina jw.
x ≥
√2 => x ≤ −
√2x2 − 4 − sprzeczność
x ≤ −√2 => x ≤ −
√2x2 − 4 /
2
x
2 ≥ 2x
2 − 4
x2 − 4 ≤ 0 => x ∊<−2; −
√2>
ponieważ
x ≤ −√2 to x ∊<−2; −
√2>
ICSP byłeś wielki, jesteś wielki i ... pozostań wielki
 pigor
pigor − twoje rozwiązania jeszcze raz przeanalizuję − jeżeli to dodatkowo mi rozjaśni − to
też będę dźwięczny

25 mar 22:49
Domel: Dzięki Mila ale trzymacie się z pigorem nierówności nr 1 a były 4
1. x − √2x2−4 ≥ 0
2. x − √2x2−4 ≤ 0
3. x + √2x2−4 ≥ 0
4. x + √2x2−4 ≤ 0
Dlatego podchodziłem do każdej nierówności osobno.
No ale posta można chyba zamykać z podziękowaniem wszystkim za zaangażowanie
25 mar 23:09
Mila:
Przepraszam, nie widziałam w tym gąszczu komentarzy.
Coś trzeba pomóc?
25 mar 23:13
Domel: Dzieki
Mila (

) − ale chyba już zrozumiałem jak to działa (mam nadzieję)
Do następnego

25 mar 23:20
Mila:
Do zobaczenia

25 mar 23:21
 trzeba kłaść się spać bo mój mózg już chrapie
trzeba kłaść się spać bo mój mózg już chrapie 

 Muszę zastrzelić
moderatora żeby to zniknęło
Muszę zastrzelić
moderatora żeby to zniknęło 


 x − √ 2x2 − 4 ≥ 0
2x2 − 4 ≥ 0
x2 ≥ 2
x ≤ − √2 lub x ≥ √2
D = ( −∞ ; − √2 > ∪ < √2 ; +∞ )
−−−−−−−−−−−−−−−−−−−−−−−
x ≥ √2 x2 − 4
Dla x ≥ √2 podnosimy obustronnie do kwadratu:
x2 ≥ 2 x2 − 4
0 ≥ x2 − 4
x2 − 4 ≤ 0 ⇔ x ∊ < − 2; 2>
zatem x ∊ < √2 ; 2 >
=================
x − √ 2x2 − 4 ≥ 0
2x2 − 4 ≥ 0
x2 ≥ 2
x ≤ − √2 lub x ≥ √2
D = ( −∞ ; − √2 > ∪ < √2 ; +∞ )
−−−−−−−−−−−−−−−−−−−−−−−
x ≥ √2 x2 − 4
Dla x ≥ √2 podnosimy obustronnie do kwadratu:
x2 ≥ 2 x2 − 4
0 ≥ x2 − 4
x2 − 4 ≤ 0 ⇔ x ∊ < − 2; 2>
zatem x ∊ < √2 ; 2 >
=================
 Wykres funkcji
y = x − √2 x2 − 4
y ≥ 0 ⇔ x ∊ < √2 ; 2 >
Wykres funkcji
y = x − √2 x2 − 4
y ≥ 0 ⇔ x ∊ < √2 ; 2 >

 No i są jeszcze przypadki:
3. x + √2x2 − 4 ≥ 0
4. x + √2x2 − 4 ≤ 0
Kurde, żeby tłumaczyć innej osobie to sam muszę to w końcu zrozumieć.
No i są jeszcze przypadki:
3. x + √2x2 − 4 ≥ 0
4. x + √2x2 − 4 ≤ 0
Kurde, żeby tłumaczyć innej osobie to sam muszę to w końcu zrozumieć.
 x≥0
x≥0



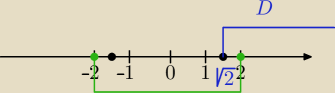 1) D:
2x2−4≥0⇔x≤−√2 lub x≥√2
2)
x≥√2x2−4 ponieważ √2x2−4 ≥0 to x>0 ( x=0 nie należy do dziedziny)
D: x∊<√2,∞)
Możemy podnieść obie trony nierówności do kwadratu
x2≥2x2−4⇔
x2−4≤0⇔x∊<−2,2> i x∊D⇔x∊<√2,2>
1) D:
2x2−4≥0⇔x≤−√2 lub x≥√2
2)
x≥√2x2−4 ponieważ √2x2−4 ≥0 to x>0 ( x=0 nie należy do dziedziny)
D: x∊<√2,∞)
Możemy podnieść obie trony nierówności do kwadratu
x2≥2x2−4⇔
x2−4≤0⇔x∊<−2,2> i x∊D⇔x∊<√2,2>
 warto napisać daną nierówność w takiej postaci równoważnej,
aby z definicji pierwiastka st. 2 wykluczyć x< 0 (zaś x=0 przez podstawienie
nie sprawdza tej nierówności) i nie mów, że ja rozpatrzyłem tylko 1−szy
przypadek ; moje rozwiązanie jest kompletne i tyle.
warto napisać daną nierówność w takiej postaci równoważnej,
aby z definicji pierwiastka st. 2 wykluczyć x< 0 (zaś x=0 przez podstawienie
nie sprawdza tej nierówności) i nie mów, że ja rozpatrzyłem tylko 1−szy
przypadek ; moje rozwiązanie jest kompletne i tyle. 

 (√a=b ≥ 0 )
(√a=b ≥ 0 )

 pigor − twoje rozwiązania jeszcze raz przeanalizuję − jeżeli to dodatkowo mi rozjaśni − to
też będę dźwięczny
pigor − twoje rozwiązania jeszcze raz przeanalizuję − jeżeli to dodatkowo mi rozjaśni − to
też będę dźwięczny 
 ) − ale chyba już zrozumiałem jak to działa (mam nadzieję)
Do następnego
) − ale chyba już zrozumiałem jak to działa (mam nadzieję)
Do następnego 
