walec
bezendu:
W stożek o promieniu podstawy długości 9 i wysokości 12 wpisano walec, w ten sposób, że jedna
podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w
powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca,
wiedząc że pole powierzchni bocznej walca wynosi 48π .
h=8 lub h=4 ?
23 mar 22:42
Alfa: tak
23 mar 22:46
bezendu:
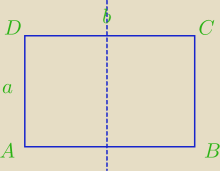
Prostokąt ABCD obracając się wokół boku AB , zakreślił walec w1. Ten sam prostokąt obracając
się wokół boku AD , zakreślił walec w2 . Otrzymane walce mają równe pola powierzchni
całkowitych. Wykaż, że prostokąt ABCD jest kwadratem
Dwa rysunki
P
1=2πb(b+a)
P
2=2πa(a+b)
2πb(b+a)=2πa(a+b)
b
2+ba=a
2+ab
b
2=a
2
b=a C.N.W ?
23 mar 22:47
bezendu:
A mogłabyś rzucić okiem na to ?
23 mar 22:50
Mila:
h=4, r=6
h=8, r=3
23 mar 22:51
Alfa: Przyjmując oznaczenia jak na rys., to raczej powinno być:
P1 = 2πa(a+b)
P2 = 2πb(b+a)
reszta bez zmian i jest OK.
23 mar 22:52
bezendu:
Wiem, że wyszły dwa rozwiązania ale ja podałem tylko wysokości bo o to pytają. Zobacz na ten
dowód ?
23 mar 22:52
bezendu:
skoro obraca się według boku a to b jest promieniem przecież
rozważamy 1 sytuację
P=2πr(r+h)
P1=2πb(b+a)
23 mar 22:54
Mila: 22:47 dobrze.
23 mar 22:54
bezendu:
Dziękuję. Mila będziesz jeszcze chwilkę na forum ?
23 mar 22:55
Mila: Tak.
Oczywiście na maturze mają byc porządne 2 szkice z oznaczeniami.
23 mar 22:56
bezendu:
Chciałem tylko ogólny zarys rozwiązania. Wiem, że na maturze muszę przedstawić dwa rysunki.
Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego
walca aby objętość się nie zmieniła?
V=πr
2h
23 mar 22:58
23 mar 23:02
bezendu:
Dziękuję jeszcze jedno zadania, wiem, że banalne i ostatnio robione na forum ale sam mam z tym
zadaniem mam problem a widziałem je w arkuszu więc muszę zrobić
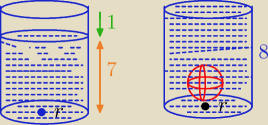
Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o
promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz
objętość naczynia. Przyjmując π ≈ 3,14 , wynik podaj z dokładnością do 1 cm 3
Tylko powiedz od czego zacząć.
23 mar 23:05
Mila:
objętość kulki=objętość walca o promieniu r=x i wysokości h=1cm.
po obliczeniu r liczysz objętość naczynia
V=πr2*8
23 mar 23:15
bezendu:
Objętość kulki=objętość walca ?
Ja do walca wrzucam kulkę i podnoszę tym samym poziom wody ?
23 mar 23:21
Mila:
Oczywiście, a wyparta woda przyjmuje kształt naczynia.
23 mar 23:22
Mila:
23 mar 23:28
bezendu:
Ja do objętości walca muszę dodać objętość kulki ?
23 mar 23:32
bezendu: ?
23 mar 23:43
Eta:
prawo Archimedesa
23 mar 23:43
bezendu:
Miałem to na fizyce wieki temu.
23 mar 23:44
Eta:
Jakie wieki? ..... ja mam teraz w 1LO
23 mar 23:45
Marcin: Eta, a który to już rok w tym 1LO, co?
23 mar 23:47
bezendu:
Wieki ciemne. A wracając do zadania to ?
23 mar 23:48
Marcin: Objętość walca dla h=1 jest równa objętości kuli.
Liczysz r walca i później możesz już wyliczyć objętość walca dla h=8
23 mar 23:48
bezendu:
A no tak dla h=1 jest równa v kulki. Ok Dziękuję
23 mar 23:49
Mila:
Nic w naturze nie ginie, tylko zmienia postać.
Pusta przestrzeń w pierwszym naczyniu została zapełniona wodą, która ma objętość wrzuconej
kulki.
23 mar 23:51
bezendu:
A skarp
Eta tak długo w lo bo na wf nie chodzi
23 mar 23:51
bezendu: Już zrozumiałem, na dziś wystarczy, dziękuję i dobranoc
23 mar 23:52
ja: Wczoraj Radek nad tym zadaniem sie głowił
24 mar 00:35