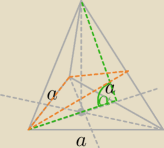
 Dany jest ostrosłyp prawidłowy trójkątny. Długość krawędzi podstawy ostrosłupa jest równa "a",
krawędź boczna jest nachylona do płaszczyzny jego podstawy pod kątem α. Ostrosłup przecięto
płaszczyzną przechodząca przez krawędź podstawy i środek przeciwległej krawędzi bocznej.
a) oblicz pole otrzymanego przekroju.
b) wyznacz sinus kąta nachylenia płaszczyzny przekroju do płaszczyzny podstawy ostrosłupa.
pomarańczowy to ta płaszczyzna która tnie ostroslup. Dobrze namalowałem?
Dany jest ostrosłyp prawidłowy trójkątny. Długość krawędzi podstawy ostrosłupa jest równa "a",
krawędź boczna jest nachylona do płaszczyzny jego podstawy pod kątem α. Ostrosłup przecięto
płaszczyzną przechodząca przez krawędź podstawy i środek przeciwległej krawędzi bocznej.
a) oblicz pole otrzymanego przekroju.
b) wyznacz sinus kąta nachylenia płaszczyzny przekroju do płaszczyzny podstawy ostrosłupa.
pomarańczowy to ta płaszczyzna która tnie ostroslup. Dobrze namalowałem?
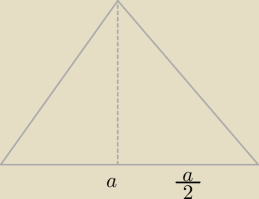 jak wyliczyć wysokość tego trójkąta pomarańczowego?
jak wyliczyć wysokość tego trójkąta pomarańczowego?
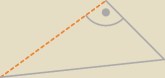 to ten trójkąt na przedniej ściance, on jest prostokątny? pomoże nam w obliczeniu krawędzi tego
trójkąta równoramiennego?
to ten trójkąt na przedniej ściance, on jest prostokątny? pomoże nam w obliczeniu krawędzi tego
trójkąta równoramiennego?

| a | R | R | a | |||||
R = | , | = cosα ⇒ b = | = | |||||
| √3 | 2b | 2cosα | 2√3cosα |
| 1 | ||
k = | a√3, z tw. kosinusów: w2 = b2 + k2 − 2bk cosα ⇒ w = | |
| 2 |
| 1 | ||
Pole przekroju P = | aw | |
| 2 |
| b | w | |||
Z twierdzenia sinusów: | = | ⇒ sinβ = ... | ||
| sinβ | sinα |
| a | ||
R = | ||
| √3 |
| 6a6+3√3a4+3a4R | ||
w=√ | ||
| 192√3cos2α*2b |
 coś nie tak pomoze ktoś?
coś nie tak pomoze ktoś?
 ?
?
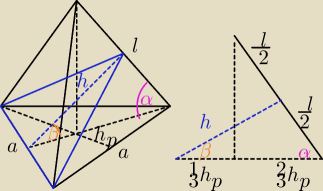 moje wyniki
moje wyniki
| a | ||
h = | tgα√3 | |
| 3 |
| a2 | ||
P = | tgα√3 | |
| 6 |
| 1 | ||
sinβ = | ||
| 2 |