plan
bezendu:
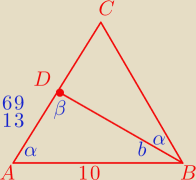
Dany jest trójkąt równoramienny ABC , w którym |AB|=|AC| i |BC|=10. Na boku AC wybrano punkt D
| | 69 | |
w ten sposób, że |∡CBD|=|∡BAC|=α oraz |AD |= |
| . Oblicz sinα . |
| | 13 | |
Kąt ABC musi być równy α skoro ΔABC jest równoramienny ?
23 mar 19:00
Marcin: U Ciebie na rysunku |AB|=10, a w treśći |BC|=10. Nie myl oznaczeń

23 mar 19:05
bezendu:
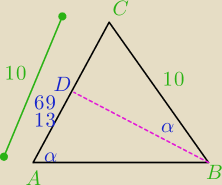
Faktycznie
23 mar 19:08
Godzio:
Oznaczenia dalej są źle. Przeczytaj jeszcze raz polecenie.
23 mar 19:11
Marcin: |BC|, to Twoja podstawa, a nie ramię. Przecież |AB|=|AC|
23 mar 19:11
bezendu:
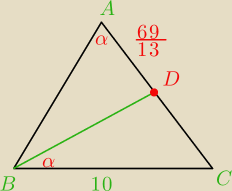
23 mar 19:15
domel:
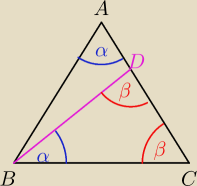
| |AD| | | |AB| | |
| = |
| |
| sin(β−α) | | sin(180−β) | |
β = 90−0,5α
23 mar 19:35
bezendu:
Gdzie w trójkącie ABD masz β ?
23 mar 19:38
domel: W trójkącie ABD samej β−ty nie ma ale są α, (β−α) i (180−β)
23 mar 19:43
bezendu:
Dzięki domelku już wiem z czego to wynika, choć ja mam podany kąt α w zadaniu i nie myślałem
szukać β
23 mar 19:53
domel:
1. Dla trójkąta ABD
| | |AB| | |
| = |
| |
| sin(90−1,5α) | | sin(90+0,5α) | |
| 69 | | |AB| | |
| = |
| |
| 13*sin(90−1,5α) | | sin(90+0,5α) | |
2. Dla trójkąta ABC
| |AB| | | 10 | |
| = |
| |
| sin(90−0,5α) | | sinα | |
| | 10*sin(90−0,5α) | |
|AB| = |
| |
| | sinα | |
No i wracamy do
1.
| 69 | | | |
| = |
| |
| 13*sin(90−1,5α) | | sin(90+0,5α) | |
| 69 | | 10*sin(90−0,5α) | |
| = |
| |
| 13*sin(90−1,5α) | | sinα*sin(90+0,5α) | |
No a dalej to przekształcenie sinusów
23 mar 19:56
domel: Pisałem w trakcie twojego posta − ale mam nadzieję, że sobie dalej poradzisz

23 mar 19:58
bezendu:
Ja nie prosiłem o rozwiązanie tylko o wskazówkę.
Kiedy można sobie dopisywać a kiedy nie ? Np w tym zadaniu dopisałem β a w innych nie ?
23 mar 19:59
mietek: chcesz się na pamięć nauczyć?
23 mar 20:01
bezendu:
@Mietek zmierz sobie gorączkę.
23 mar 20:02
mietek: gorączka sobotniej nocy już mi minęła

23 mar 20:21
bezendu:
No chyba nie bo jeszcze cały czas bredzisz.

23 mar 20:22
mietek: To ty zadajesz pytania jakbyś się chciał na pamięć nauczyć. Każdy przypadek jest oddzielny i
nie ma czegoś takiego jak reguła gdzie stosować, a gdzie nie....
23 mar 20:27
bezendu:
Ja nie mam zamiaru uczyć się na pamięć...
23 mar 20:30
mietek: To nie zadawaj takich pytań, tylko staraj się analizować każde zadanie w zależności od tego co
szukasz, a potem co masz podane (w tej kolejności).
23 mar 20:31
bezendu:
Mietek dzięki za radę. Raz się przydałeś.
23 mar 20:31
Domel: bezendu pamiętaj, że możesz zawsze nazwać po swojemu jakąś niewiadomą. Czasem ją
wykorzystasz czasem nie. Ja na przykład przy zadaniach tekstowych doradzam wypisanie
WSZYSTKICH możliwych równań dotyczących zadania pomimo, że z niektórych może nie skorzystamy.
Tak samo z kątami i np. bokami − N I K T ci nie może zabronić nadania nazwy jakiemuś
niewiadomemu kątowi lub bokowi − może to później wykorzystasz a może nie ale masz od czego
zacząć.
I sorki za moją nadgorliwość z zadaniem

23 mar 22:15
bezendu:
Nie masz za co przepraszać, tylko często jak sobie dopisuję to wychodzi błąd bo mam podane
tylko a czy kąt w zadaniu a u mnie w odp zawsze coś więcej i nie wiem jak znaleźć złoty środek
na to a mam na to 40 dni !
23 mar 22:18
Domel: Zobacz, że zawsze można znaleźć jakąś zależność − np. tu dopisaliśmy kąt β ale z zależności
kątów w trójkącie już mamy, że 2β=180−α − no i wracamy do naszego zadanego kąta.
Zadania są tak z reguły układane, żeby można było znaleźć odpowiednie zależności − no czasem
trzeba zabawić się w Sherlocka Holmesa

23 mar 22:23
bezendu:
Dziękuję za odpowiedź
23 mar 22:26
Domel: Jeżeli chcesz się zabawić w Sherlocka to spróbuj rozwiązać układ 2 równań z 3 niewiadomymi
| ⎧ | V1*(T+1)=V2*(T+0,25) | |
| ⎩ | V1*(T−0,4)=V2*(T−0,8) |
|
23 mar 22:48
bezendu:
To i tak coś będzie zależne od czegoś ? Zobacz do mojego tematu z bryłami jak możesz ?
23 mar 22:50
Domel: Podaj adres twojego tematu − bo masz ich kilka
Zajrzę zaraz po Spartakusie

23 mar 23:02
bezendu:
Już Alfa i Mila rozwiały moje wątpliwości. Dziękuję za zainteresowanie

Jutro zrobię to
zadanie od Cb.
23 mar 23:09
 Dany jest trójkąt równoramienny ABC , w którym |AB|=|AC| i |BC|=10. Na boku AC wybrano punkt D
Dany jest trójkąt równoramienny ABC , w którym |AB|=|AC| i |BC|=10. Na boku AC wybrano punkt D

 Faktycznie
Faktycznie








 Jutro zrobię to
zadanie od Cb.
Jutro zrobię to
zadanie od Cb.