Tryg. Justyna: to znowu ja napotkałam na pewien problem przy rozwiązywaniu n tego zadania mianowicie po obliczeniu zmiennej t, pozostaly mi dwie nierownosci do rozwiazania, z jednej glownej(wyjsciowej),ktora przybiera postac: cosx≤1−2cos²x a oto te dwie nierownosci: cosx≤1/2 oraz cosx≤−1 Mam problem z ustaleniem , do jakiego zbioru nalezy x, w odpowiedziach powinno wyjsc <π/3+2kπ,7π/3+2kπ>dziekuje z gory za odpowiedz

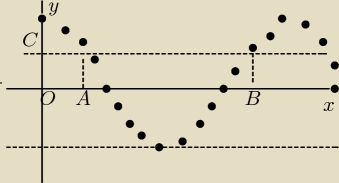
AS: Odcinek OC = 1/2 Funkcja cosx przyjmuje wartości 1/2 dla kątów π/3 (w A) i 5*π/3 (w B) Na całym odcinku AB funkcja przyjmuje wartości mniejsze lub równe od 1/2 do dolnej wartości −1 (najmniejszej jaką funkcja cosx może przyjąć). Rozwiązaniem dla pierwszego odcinka jest przedział <π/3,5*π/3> Sytuacja się powtórzy gdy przesuniemy się w prawo o kąt = 2*π. a następnie 4*π , 6*π itd Zwiększając kąt pierwotny o 2*k*π (k ∊ C) otrzymamy jako rozwiązanie przedział <π/3 + 2*k*π,5*π/3 + 2*k*π> cosx <= −1 zachodzi tylko dla x = π + 2*k*π , k ∊ C ale wartość ta mieści się w znalezionym przedziale poprzedniej nierówności.

Justyna: Rozumiem, lecz dlaczego w odpowiedziach jest 7π/3?nie jestem w stanie tego pojac.

AS: Przypuszczalnie błąd 7π/3 = π/3 + 2*π jest początkową wartością drugiego odcinka