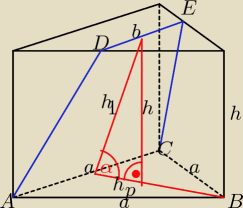
 W prawidłowym graniastosłupie trójkątnym poprowadzono płaszczyznę
przez krawędź dolnej podstawy oraz środek ciężkości podstawy górnej. Płaszczyzna ta nachylona
jest do płaszczyzny dolnej podstawy pod kątem 30 stopni. Oblicz objętość graniastosłupa,
wiedząc, żę pole otrzymanego przekroju jest równe 10.
W prawidłowym graniastosłupie trójkątnym poprowadzono płaszczyznę
przez krawędź dolnej podstawy oraz środek ciężkości podstawy górnej. Płaszczyzna ta nachylona
jest do płaszczyzny dolnej podstawy pod kątem 30 stopni. Oblicz objętość graniastosłupa,
wiedząc, żę pole otrzymanego przekroju jest równe 10.
 1
1
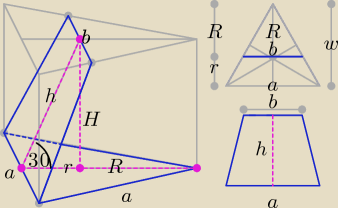 Wskazówki:
Środek ciężkości w trójkącie to punkt przecięcia środkowych.
Wskazówki:
Środek ciężkości w trójkącie to punkt przecięcia środkowych.
| 1 | ||
r = | a√3 | |
| 6 |
| 1 | ||
R = | a√3 | |
| 3 |
| 1 | ||
R + r = w, w = | a√3 | |
| 2 |
| 1 | |
(a + b)h = 10 | |
| a |

| 1 | ||
Jeszcze chochlika przegonię, | (a + b)h = 10  | |
| 2 |
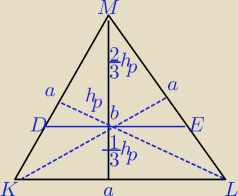 Dane: P = 10 (pole przekroju ACED)
α = 300
−−−−−−−−−−−−−−−−−−−−−−
Dane: P = 10 (pole przekroju ACED)
α = 300
−−−−−−−−−−−−−−−−−−−−−−
| a2√3 | ||
V= ? V= Pp *h = | * h | |
| 4 |
| a | hp | a | 3 | 2 | |||||||||||
= | ⇒ | = | ⇒ 2a = 3b ⇒ b = | a | |||||||||||
| b |
| b | 2 | 3 |
| h | ||
Z czerwonego trójkąta (rys.1) : | = sinα | |
| h1 |
| h | ||
= sin 300 | ||
| h1 |
| h | 1 | |||
= | ⇒ h1 = 2h | |||
| h1 | 2 |
| ||||||||
Z tego samego trójkąta: | = cosα | |||||||
| h1 |
| ||||||||||||||
= cos300 | ||||||||||||||
| h1 |
| a√3 | √3 | √3 | ||||
= h1 * | /: | |||||
| 6 | 2 | 2 |
| a | ||
h1 = | ||
| 3 |
| a | ||
Czyli z przyrównania ostatnich 2 wyników mamy: 2h = | ⇒ a = 6h | |
| 3 |
| 1 | ||
P = | (a + b) * h1 | |
| 2 |
| 1 | 2 | a | ||||
10 = | (a + | a) * | ||||
| 2 | 3 | 3 |
| a | 2 | |||
10 = | (a + | a) | ||
| 6 | 3 |
| a2 | 2a2 | |||
10 = | + | |||
| 6 | 18 |
| 3a2 + 2a2 | ||
10 = | /*18 | |
| 18 |
| a | 6 | |||
a = 6h ⇒ h = | = | = 1 | ||
| 6 | 6 |
| a2√3 | 62 * √3 | 36√3 | ||||
V = | * h = | * 1 = | = 9√3 [j3] | |||
| 4 | 4 | 4 |
