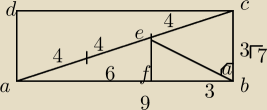
 W prostokącie ABCD, w którym |AB|=9, |AD|=3√7, na przekątnej AC wybrano taki punkt E, że
|AE| : |EC|=2:1. Oblicz sinus kąta ∡EBC.
Obliczam przekątną |AC|
|AC|=12
Teraz patrząc na rysunek widzę, że jeśli bok |AE| 2:1 |EC|
to:
bok |AF|=6 |FB|=3
bok |AE|=8 |EC|=4
bok |CB|=3√7 |EF|=2√7
Obliczam teraz bok |EB| korzystając z tw. Pitagorasa:
|EB|=√37
Mam wszystkie boki trójkąta EBC
Wykorzystam teraz twierdzenie cosinusów:
42=√372+(2√7)2−2*√37*2√7*cosα
16=37+63−6√259*cosα
W prostokącie ABCD, w którym |AB|=9, |AD|=3√7, na przekątnej AC wybrano taki punkt E, że
|AE| : |EC|=2:1. Oblicz sinus kąta ∡EBC.
Obliczam przekątną |AC|
|AC|=12
Teraz patrząc na rysunek widzę, że jeśli bok |AE| 2:1 |EC|
to:
bok |AF|=6 |FB|=3
bok |AE|=8 |EC|=4
bok |CB|=3√7 |EF|=2√7
Obliczam teraz bok |EB| korzystając z tw. Pitagorasa:
|EB|=√37
Mam wszystkie boki trójkąta EBC
Wykorzystam teraz twierdzenie cosinusów:
42=√372+(2√7)2−2*√37*2√7*cosα
16=37+63−6√259*cosα
| 84 | 14√259 | 2√259 | ||||
cosα= | = | = | ≈ 0,87 | |||
| 6√259 | 259 | 37 |
 Mógłby ktoś sprawdzić? Byłbym ogromnie wdzięczny.
Mógłby ktoś sprawdzić? Byłbym ogromnie wdzięczny.