kąt dwuścienny, objętość graniastosłupa Miłosz: 1. W szcześcianie ABCDEFGH przekątna podstawy BD i wierzchołek E wyznaczają płaszczyznę BDE, natomiast przekątna BD i wierzchołek G wyznaczają płaszczyznę BDG. Oblicz miarę kąta dwuściennego wyznaczonego przez te płaszczyzny. cosα powinien wyjść 1/3 2. Podstawą graniastosłupa prostego ABCDEFGH jest prostokąt 3cm². Trójkąty BCE oraz CDE, w których BE oraz DE są przekątnymi ścian bocznych, a CE jest przekątną graniastosłupa, są nachylone do podstawy odpowiednio pod kątem o mierze 30stopni oraz 60stopni. Oblicz objętość graniastosłupa. W OBYDWU ZADANIACH BARDZO PROSIŁBYM O RYSUNKI, ponieważ nie do końca wiem jak to zilustrować, szczególnie w zad 2.

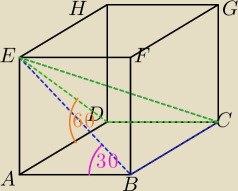
dero2005: zad 2 AB*AD = 3

EA
	= tg30o
AB

EA
	= tg60o
AD

EA =

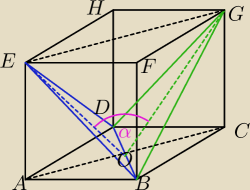
dero2005: AB = BC = CD = DA = EF = FG = GH = HE = AE = BF = CG = DH = a EG = AC = d = a√2

	√6
OG = OE = h = √(a√22)2 + a2 = a
	2

d² = 2h² − 2h²cosα

	1
cosα =
	3

Miłosz: DZIĘKUJĘ BARDZO, JUŻ WSZYSTKO ROZUMIEM!