kwadrat kasia: Na odcinku AB o długości 20 cm obrano punkt C i zbudowano dwie figury. Wyznacz położenie punktu C tak aby suma tych figur była najmniejsza jeżeli te figury to: a) kwadrat o boku AC i kwadrat o boku BC b) kwadrat o boku AC oraz półkole o średnicy BC c) kwadrat o boku AC oraz trójkąt równoboczny o boku BC

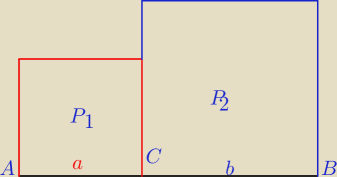
Janek191: a) a = i AC I b = I BC I = 20 − a S = P₁ + P₂ = a² +(20 − a)² = a² + 400 − 40 a + a² = 2 a² − 40 a + 400 S(a) = 2 a² − 40 a + 400

	40
Funkcja ta przyjmuje najmniejszą wartość dla a = p =		= 10
	4

Wtedy I AC I = I BC I = 10 =====================

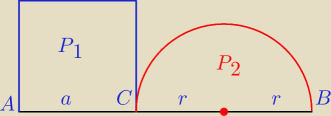
Janek191: b) Mamy a + 2 r = 20 ⇒ a = 20 − 2 r więc S = P₁ + P₂ = a² + 0,5 π r² = ( 20 − 2 r)² + 0,5 π r² = 400 − 80 r + 4 r² + 0,5 π r² S( r) = ( 4 + 0,5 π) r² − 80 r + 400 4 + 0,5 π > 0 , więc

	80
funkcja S(r) przyjmuje najmniejszą wartość dla r = p =		≈ 7,2
	8 + π

	160
Wtedy I BC I = 2 r =		≈14,4
	8 + π

=================================

kasia: a skąd wiesz że 4+0,5π >0 ? i nie rozumiem tego dalszego zapisu, mógłbyś mi wytłumaczyć?

Janek191: π ≈ 3,14, więc 4 + 0,5 π ≈ 4 + 0,5*3,14 ≈ 4 + 1,57 = 5,57 > 0 Jeżeli współczynnik przy r² jest > 0 , to ramiona paraboli ( wykresu funkcji S(r) =(4 +0,5π)r² − 80r + 400 ) są skierowane ku górze i funkcja

	80		80
osiąga najmniejszą wartość q dla r = p =		=
	2*( 4 + 0,5 π)		8 + π