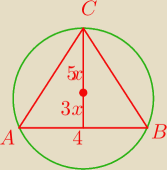
okrąg bezendu: Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta. ?

bezendu: ?

jakubs: 5x=r i z tw pitagorasa 25x²=9x²+4 Dobrze myślę ?

bezendu: Nie wiem czy dobrze myślisz ? Ale zobaczymy co z tego wyjdzie

bezendu: 16x²=4

	1
x2=
	4

	1
x=
	2

Ale skąd Ty masz takie równanie ?

jakubs: Od środka okręgu opisanego do pkt C jest 5x, to jest taka sama odległość jak do pkt B.

Marcin: Według mnie, to 3x=r. P=2*8x=16x

	abc
P=
	4R

P=rp bc=2c² abc=8c² p={4+2c}{2} p=2+c Znasz wzory, wszystko masz. Próbuj może tak

bezendu: Skąd masz to: 25x²=9x²+4 ?

jakubs: No w treści zadania jest 3:5, więc no wygląda na to jak pisze Marcin.

bezendu: Ale ja się pytam o Twoje równanie bo z tego wychodzi poprawnie. Marcina wpisu jeszcze nie znalizowałem

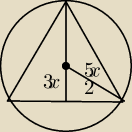
jakubs: Poprowadź prostą ze środka okręgu opisanego do punktu B. I ta odległość jest równa odległości środka okręgu opisanego do punktu C. Oznaczmy to jako r−promien r=5x Teraz z twierdzenia pitagorasa w tym małym trójkącie prostokątnym o przyprostokątnych 2,3x i przeciwprostokątnej 5x układam równanie 25x²=2²+9x²

mietek: dlaczego słowo "jedną" uważacie za tę którą najłatwiej wybrać? przecież wysokości nie są równej długości....

mietek: za to się odejmuje punkty....

Saizou : Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych jego boków, a tylko jest jeden odcinek który jest symetralną boku i wysokością

mietek: nie prawda... "środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych jego boków, a tylko jest jeden odcinek który jest symetralną boku i wysokością" − to jest bzdura.