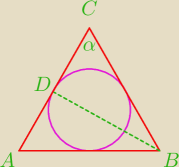
Okrąg bezendu: W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC | = |BC | = b oraz |∡ACB | = α . Z wierzchołka B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok AC w punkcie D . Oblicz promień okręgu wpisanego w trójkąt ABC oraz długość odcinka BD czy kąt ADB=90⁰

	bcosα
r=
	2+√2+2cosα

bezendu: ?

Mila: W treści masz " przez środek okręgu opisanego" , na rysunku masz okrąg wpisany. Środek okręgu wpisanego leży na przecięciu dwusiecznych kątów. Tylko dwusieczna kąta α jest prostopadła do boku.

bezendu: a promień dobry ?

Mila: Liczę.

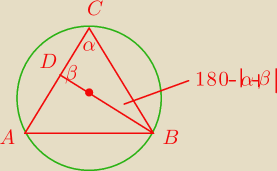
bezendu: Z twierdzenia sinusów

b		|DB|
	=
sinβ		sinα

bsinα=|DB|sinβ

	bsinα
|DB|=
	sinβ

?

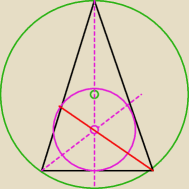
...: ... jak widzisz nie Środek okręgu wpisanego wyznacza punkt przecięcia się dwusiecznych

bezendu: @... a co mi to daję ?

Mila: Mam inny wynik. Napisz obliczenia.

Mila:

	α
Masz dużo danych, łatwo obliczasz a, albo z sin		( poprowadź wysokość do AB), albo tw.
	2

cosinusów. Porównujesz pole Δ , otrzymujesz r.

Mila: Dobranoc

bezendu:

	1
P=		*b*b*sinα
	2

	b2sinα
P=
	2

długość 3 boku z twierdzenia cos x²=b²+b²−2*b*b*cosα x²=2b²−2b²cosα x²=b²(2−2cosα) x=b√2−2cosα

	2P
r=
	a+b+c

r=U{b²sinα}{b+b+b√2−2cosα

	b2sinα
r=
	2b+b√2−2cosα

	b2sinα
r=
	b(2+√2−2cosα

r=U{bsin²}{2+√2−2cosα ?

bezendu: Nie wiem nadal jak policzyć DB ?

Mila: r dobrze, w ostatniej linijce literówka. Jutro DB.

Mila: Z tw. sinusów.

bezendu: Ok, dziękuję

bezendu: Z twierdzenie sinusów wychodzi tak jak podałem, ale taka nie może być odp bo w treści mam tylko α i b

bezendu: Skoro mam dobrze policzone r, to jak obliczyć |BD| ?

bezendu: Proszę o wskazówkę jak policzyć BD ?

marta: |<BDC|= 1,5α z tw. sinusów w trójkącie BDC : |BD|=......

bezendu: Jakim cudem |<BDC|=1,5α ?

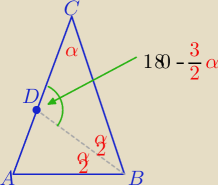
marta: sorry ..=180^o−1,5α

bezendu: A skąd wiadomo, że odcinek BD dzieli kąt ABC na pół ?

marta: To przecież dwusieczna!

bezendu: Skąd mam wiedzieć, że to dwusieczna, skoro nie ma mowy o tym w zadaniu !

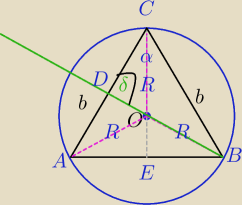
Mila: DB przechodzi przez środek okręgu opisanego na ΔABC CE jest dwusieczną kąta α ΔCOB− Δrównoramienny

DB		b
	=
sinα		sinδ

Wyrazić δ w zależności od α

	1
δ+α+		α=180
	2

dalej sam.

Mila: DB nie jest dwusieczną kąta B.

bezendu:

	3
To skąd tam u Ety 180−		α ?
	2

marta: Sorry nie doczytałam zadania

marta:

bezendu:

	1
A ta zależność δ+α=		α to w trójkącie DOC ?
	2

bezendu: ?

marta: Zapytaj Milę ...... narysowała, to Ci podpowie

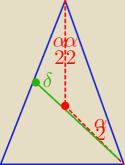
Mila: W ΔCOB:

	1
∡OBC=		α, bo Δ jest równoramienny.
	2

W ΔDBC:

	1
δ+α+		α=180 z sumy kątów w Δ.
	2

Dalej tw. sinusów w tym Δ

bezendu:

	1
Nadale nie wiem czemu BDC jest		α skoro BD nie jest dwusieczną
	2

Mila: 17:30 masz napisane, czytaj i patrz na rysunek. Eta narysowała .

bezendu: Czytam wszystkie posty. Rysunek też widziałem.

Mila: CE jest dwusieczną kąta α. ( wiadomo dlaczego?) ΔCOB jest równoramienny (boki: R,R, b) kąty pprzyległe do boku b to U{α}{2,U{α}{2

bezendu: Dziękuję, teraz wszystko jasne.

Mila: Licz.

bezendu:

	bsinα
DB=		i już coś człowiek zaczyna rozumieć dzięki takiej pomocy
	3α   sin   2

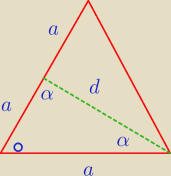
bezendu: Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość d W miejscu kropki 180−2α I z twierdzenia sinusów ?

bezendu: Coś chyba nie tak bo w odp mam teraz cosα a w zadaniu miałem tylko d podane

Mila: Nie znasz kąta. 1) oblicz cosinus kąta między ramionami Δ− tw. cosinusów do ΔABC. 2) tw. cosinusów do górnego Δ.

zombi: Dwa razy tw. cosinusów dla kąta kropeczka. Tzn. pierw dla małego trójkąta a później dla całości.

zombi: Ew. tw. Stewarta, fajny wzorek, w którym już masz te dwa tw. cosinusów.

bezendu: @zombie skąd wziąłeś to twierdzenie ?

zombi: Z książek http://en.wikipedia.org/wiki/Stewart%27s_theorem

Piotr 10: Po częsci podobne to tw. o dlugosci dwusiecznej kąta

bezendu: Dobre to ale policzę ''tradycyjnie'' tak jak radzi Mila

bezendu: (2a)²=(2a)²+a²−2*2a*a*cosα 4a²=5a²−4a²cosα

	1
cosα=
	4

I teraz co mam wyliczyć ?

Mila: Obliczyłeś cosinus kąta przy podstawie. Teraz tw. cosinusów :

	1
d2=a2+a2−2a*a*
	4

licz a, potem obwód Δ

bezendu: OK.

	1
d2=2a2−		a2
	2

d²=1,5a²

	√6
d=		a
	2

	√6
a=		d
	3

Obw=5a

	5√3
Obw=		d
	3

Tylko czemu mam dwa razy liczyć Z cosinusów ?

Mila: Najpierw obliczyłeś cos α, potem a. Mogłeś z tw. Pitagorasa obliczyć a.

bezendu: A gdzie kąt prosty żeby pitagorasa liczyć ?

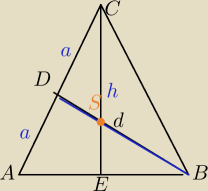
Mila: Musisz zrobić dobry rysunek . Narysować wysokość, obliczyć. Skorzystać, że środkowe przecinają się w jednym punkcie i dzielą w stosunku 2:1. Znowu tw. Pitagorasa.

	1
h2=(2a)2−(		a)2
	2

h=...

	1
SE=		h
	3

	2
SB=		d
	3

	1
EB=		a
	2

SB²=SE²+EB² i to chyba więcej roboty niż poprzednio, a może nie? Zrób tak.

bezendu: To jednak pierwsza opcja lepsza.