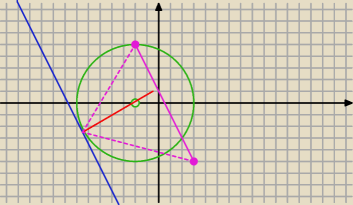
geometria analityczna razor: Dane są punkty A(−2,5), B(3,−5). Punkt C należy do okręgu o równaniu (x+2)² + y² = 25. Znajdź współrzędne tego punktu C, tak aby pole ABC było maksymalne. Oblicz to pole wyznaczylem |AB| = 5√5, prosta przechodzaca przez te punkty y = −2x + 1. Punkt C(x_c,y_c) musi spelniac rownanie okregu i odleglosc punktu C od prostej y = −2x + 1 musi byc maksymalna.

	|2xc + yc − 1|
licze te odleglosc i wychodzi mi		teraz pytanie co dalej? nie chce
	√5

rozwiazania tylko wskazowki

zombi: Aby było największa to wysokość, czyli prosta ⊥ do AB musi przejść przez środek okręgu. Wtedy dostajesz równanie prostej prostopadłej do AB i przyrównujesz je z równaniem okręgu, dostajesz dwa punkty przecięcia i wybierasz ten dla którego pole będzie większe.

razor: hmm w sumie to jest logiczne i nawet widac z rysunku ale gdybym mial uzasadnic to dlaczego ta prosta musi przejsc przez srodek okregu?

Radek: Największa długość w okręgu to średnica..

razor: ok dzieki za wskazowke zombi juz rozumiem wszystko

...: