 Witam zacne grono forumowiczów
Posiadam ciekawe zadanie z optymalizacji, ale poproszę bez pochodnych
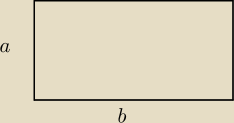
Działkę w kształcie prostokąta o powierzchni S = 900 m2 należy ogrodzić ze wszystkich stron
tak, by koszt ogrodzenia był najniższy. Jakie powinny być wymiary tej działki, jeśli jeden bok
ogrodzimy parkanem w cenie 140 Є/m, a pozostałe boki siatką w cenie 20 Є/m?
Podaj ten najniższy koszt
Witam zacne grono forumowiczów
Posiadam ciekawe zadanie z optymalizacji, ale poproszę bez pochodnych
Działkę w kształcie prostokąta o powierzchni S = 900 m2 należy ogrodzić ze wszystkich stron
tak, by koszt ogrodzenia był najniższy. Jakie powinny być wymiary tej działki, jeśli jeden bok
ogrodzimy parkanem w cenie 140 Є/m, a pozostałe boki siatką w cenie 20 Є/m?
Podaj ten najniższy koszt
| 900 | ||
ab=900→b= | a<b a∊(0:900) | |
| a |
| 3600 | ||
160a+ | ||
| a |
| 36000 | ||
160a+ |  | |
| a |



| 36 000 | ||
160a+ | = | |
| a |
| 160a2+36 000 | |
= | |
| a |
| a2+225 | ||
160( | )= | |
| a |
| (a−15)2+30a | ||
160 | = | |
| a |
| (a−15)2 | ||
160[ | +30] | |
| a |