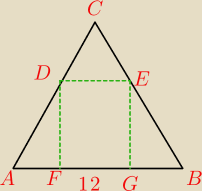
bryły Radek: W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni

	4
bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi		objętości
	9

stożka.

	4		1
πr2h=		*		*π2h
	9		3

	4
To wszystko się upraszcza i mam		więc nie mam nic
	27

Prosze o naprowadzenie gdzie robię błąd nie chcę gotowca

Radek: ?

Radek: ?

kika: Przecież h_w≠h_s i to samo z r

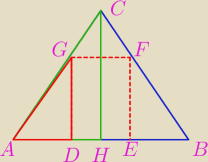
bezendu: Z nieszczęsnego podobieństwa trzeba inaczej się nie da zielony do czerwonego

Radek: To już chyba wiem jak wyliczyć.

kika: Nie odpowiadasz na wskazówki podane!

Radek: A co mam odpowiadać. Mam wskazówkę to próbuję liczyć Nie mam zdolności jednoczesnego pisania i rozwiązywania zadanie przepraszam.

Radek: Z podobieństwa mam

6−r		h
	=
6		H

H(6−r)=6h H=U{6h}{6−r) ?

bezendu: ok i dalej

Radek: Dziękuję, policzone

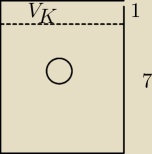
Radek: Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz objętość naczynia. Przyjmując π ≈ 3,14 , wynik podaj z dokładnością do 1 cm 3 . A tutaj ?

kika: OBJĘTOŚĆ WYPARTEJ WODY =v_p{KULKI}

kika:

Radek: Ja muszę obliczyć objętość walca więc V=πr²h h=8 jak r ?

kika:

	4
π*r2*1=		π33
	3

Radek: A czemu to ma się równać objętości kulki ? ja kulkę wrzuciłem

kika: I skup się na zadaniu, pomyśl

Marcin: Radek przecież Ci to zadanie już tłumaczyłem

kika: I kulka podniosła poziom wody o 1 cm

Radek: Ok, już mam

kika: Dziękuję , wypada też napisać.

Radek: Dziękuję !