hmm

hmm Barry: W półkole o promieniu r wpisano trapez równoramienny o przekątnej długości d . Oblicz długość krótszej podstawy trapezu.

22 mar 20:00

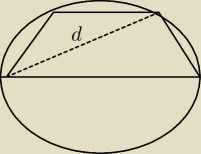
Barry: rysunek

22 mar 20:16

Piotr 10: Jeden z katów jest oparty na średnicy, czyli ma miarę 90⁰

22 mar 20:18

Piotr 10: Jest to półkole, a więc długość dłuższej podstawy wynosi 2r

22 mar 20:19

Barry: tak to wiem . Jak obliczyć dlugość krótszej ?

22 mar 20:20

Piotr 10: no to liczysz z tw. pitagorasa d²+c²=4² c − długość ramienia potem z tw. kosinuów d²=(2r)²+c² − 2*2r*c*cosα i teraz znajdź cosα z trójkąta prostokątnego i skróci Ci się parametr c i bitwa wygrana

22 mar 20:22

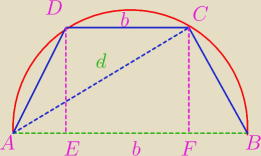
bezendu: rysunek

Przeczytałeś treść półkole a nie koło !

\|AF\|		\|AC\|
	=
\|AC\|		\|AB\|

d²=|AF|*|AB|

	d²−2r²
b=
	r

22 mar 20:22

Piotr 10: d²+c²=(2r)² powinno być na samym początku

22 mar 20:23

Piotr 10: O co chodzi?

22 mar 20:24

bezendu: mój post był do rysunku Barrego

22 mar 20:24

Piotr 10: a Ok

22 mar 20:27

Barry: bezendu już wiem o co chodzi emotka

Dziękowa za pomoc

22 mar 20:30