Dla jakich wartości parametru m∊R wierzchołek paraboli y=x^2-2(m-1)x-m leży najb Tomaszz: Witam, Mam problem z takim oto zadaniem. Tzn pewnie jest proste ale nie wiem jakie trzeba tu zrobić założenie Zad. Dla jakich wartości parametru m∊R wierzchołek paraboli y=x²−2(m−1)x−m leży najbliżej osi OX

J: Najbliżej, tzn. na niej. Warunek : Δ = 0

Tomaszz: ... domyślałem się że to jest proste, nawet banalne Dziękuję bardzo !

Tomaszz: A można jeszcze wiedzieć jaka odpowiedz wychodzi, bo nie ma nigdzie tego zadania

J: Rozwiąż równanie: [−2(m−1)]² − 4(−m) = 0

Bogdan: Przemyśl J swoją podpowiedź

Tomaszz: To już zrobiłem, wyszło mi dla m₀=3/2

Uczę się: bez "=0"

Tomaszz: @Uczę się Nie rozumiem o co chodzi, w taki razie jakie powinno być to założenie ?

Bogdan: Minimalna wartość ma osiągnąć y_w,

	−Δ
yw =		→ minimum
	4a

Uczę się: chodziło mi o podpowiedź J, bo zaczął liczyć Δ i dał do tego =0

Tomaszz: Czyli w taki razie y_w=−Δ/4a≥0

Bogdan: Δ = 4(m − 1)² + 4m = 4m² − 4m + 4

	4m2 − 4m + 4
yw =		= −m2 + m − 1
	−4

f(m) = −m² + m − 1 osiąga minimum dla m = ...

Tomaszz: to wychodzi Δ_m<0 czyli brak rozwiązań

J: "Bogdan" .... przeczytaj uważnie treść zadania

Bogdan: Ech J

	−1		1
Funkcja f(m) = −m2 + m − 1 osiąga minimum dla m =		=
	2*(−1)		2

Tomaszz: jak to mogło wyjść jak f(m) = −m² + m − 1 to Δ=1−4*(−1)*(−1) <0

J: Tu nikt nie pyta o minimum funkcji, tylko o najmniejszą odległość wierzchołka od osi OX

Bogdan: d − szukana odległość wierzchołka od osi x d = |y_w| ⇒ d = |−m² + m − 1| → minimum ⇒ d = |f(m)| → minimum d jest najmniejsze wtedy, gdy najmniejszą wartość osiąga |−m² + m − 1|,

	1
d = |−m2 + m − 1| jest najmniejsze dla m =		.
	2

W poprzednich wpisach nie użyłem wartości bezwzględnej, teraz to prostuję.

J: Kiedy odległość punktu od prostej jest najmniejsza ? Gdy wynosi 0 , czyli punkt lezy na prostej A więc: y_w = 0 lub Δ = 0

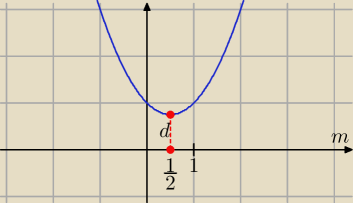
Bogdan: To jest wykres d = |−m² + m − 1|

Bogdan: Podaj J rozwiązanie swojego rozumienia zadania, czyli podaj rozwiązanie Δ = 0

J: I kiedy "d" ma najmniejszą wartość ? Gdy d = 0 , czyli wierzchołek leży na osi OX.

Bogdan: Powtarzam − podaj J rozwiązanie swojego rozumienia zadania, czyli podaj rozwiązanie Δ = 0

J: Dobra.. Przekonałeś mnie Pozdrawiam