Funkcja kwadratowa
Skejcik: Mam problem z zadaniem nie rozumiem w ogóle jak to "zobaczyć".
Nawet nie potrafię tego narysować z tym "m"
Znajdź te wartości parametru m, dla których funkcja y=x2+mx+9 ma dwa miejsca zerowe większe od
2.
A co gdyby miała mieć miejsca pomiędzy?
A co gdyby miała mieć mniejsze? Jak to zobaczyć?
22 mar 13:18
Skejcik: Mógłby ktoś mi to wyjaśnić..
22 mar 15:21
Uczę się: aby funkcja miała 2 miejsca zerowe to
Δ>0, x1 > 2, x2 > 2
i rozwiązujesz każdy z tych założeń. Oczywistym jest że abyś mógł policzyć dwie nierówności to
musisz się dowiedzieć czy wgl Δ> 0
22 mar 15:30
Bogdan:
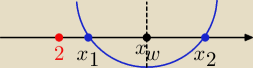
x
1 > 2 i x
2 > 2 dla f(x) = x
2 + mx + 9, x
w − odcięta wierzchołka paraboli
Założenia: Δ > 0 i f(2) > 0 i x
w > 2
22 mar 15:35
Skejcik: i tu pojawia się mój problem. Jak wy widzicie to, że funkcja
f(2)>0 skąd to bierzecie? Tego za nic nie mogę zrozumieć. Bardzo proszę o pomoc.
22 mar 16:23
J: Zauważ,że gdyby f(2) ≤ 0 , to x1 albo wynosiłoby 2 dla f(2) = 0 lub byłoby mniejsze od 2
22 mar 16:27
Skejcik: Jak mam to zauważyć?
Jak podstawiam f(2)=13+2m i nic mi to nie mówi
22 mar 16:58
Utem:
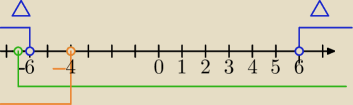
f(x) = x
2 + mx + 9,
Warunki, które podał Ci p.
Bogdan
1) Δ>0
Δ=m
2−4*9=m
2−36
m
2−36>0⇔
m<−6 lub m>6
i
2) f(2)>0⇔
| | 13 | |
22+2m+9>0⇔2m>−13⇔ m>− |
| |
| | 2 | |
i
Teraz na osi zaznaczamy i szukamy części wspólnej.
22 mar 17:21
Skejcik: Przepraszam jeżeli źle się wyraziłem, ja nie rozumiem tylko jednego podpunktu:
f(2)>0
Jak go zobaczyć? Nie potrafię tego zrobić o niczym mi nie mówi. Nie potrafię go sobie wyobrazić
i obliczyć.
22 mar 17:26
Bogdan:
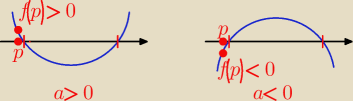
y = ax
2 + bx + c, x
1 − x
2 to miejsca zerowe
Jeśli x
1 > p i x
2 > p to a*f(p) > 0, w tym zadaniu a = 1 i p = 2, więc 1*f(2) > 0
a*f(p) = 0 i a ≠ 0 oznacza, że f(p) = 0 i x
1 = p
a*f(p) < 0 i a ≠ 0 oznacza, że x
1 < p, p jest wtedy na osi po prawej stronie x
1
22 mar 17:44
Bogdan:
x1, x2 − miejsca zerowe
22 mar 17:44
 x1 > 2 i x2 > 2 dla f(x) = x2 + mx + 9, xw − odcięta wierzchołka paraboli
Założenia: Δ > 0 i f(2) > 0 i xw > 2
x1 > 2 i x2 > 2 dla f(x) = x2 + mx + 9, xw − odcięta wierzchołka paraboli
Założenia: Δ > 0 i f(2) > 0 i xw > 2
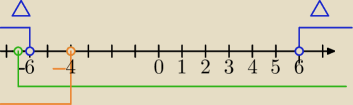 f(x) = x2 + mx + 9,
Warunki, które podał Ci p.Bogdan
1) Δ>0
Δ=m2−4*9=m2−36
m2−36>0⇔m<−6 lub m>6
i
2) f(2)>0⇔
f(x) = x2 + mx + 9,
Warunki, które podał Ci p.Bogdan
1) Δ>0
Δ=m2−4*9=m2−36
m2−36>0⇔m<−6 lub m>6
i
2) f(2)>0⇔
 y = ax2 + bx + c, x1 − x2 to miejsca zerowe
Jeśli x1 > p i x2 > p to a*f(p) > 0, w tym zadaniu a = 1 i p = 2, więc 1*f(2) > 0
a*f(p) = 0 i a ≠ 0 oznacza, że f(p) = 0 i x1 = p
a*f(p) < 0 i a ≠ 0 oznacza, że x1 < p, p jest wtedy na osi po prawej stronie x1
y = ax2 + bx + c, x1 − x2 to miejsca zerowe
Jeśli x1 > p i x2 > p to a*f(p) > 0, w tym zadaniu a = 1 i p = 2, więc 1*f(2) > 0
a*f(p) = 0 i a ≠ 0 oznacza, że f(p) = 0 i x1 = p
a*f(p) < 0 i a ≠ 0 oznacza, że x1 < p, p jest wtedy na osi po prawej stronie x1