cosx
Damian: cos4x − jak to przekształcić ? nie wiem gdzie szukać wzorów redukcyjnych kąta poczwórnego
z góry dziękuj !
21 mar 15:54
Saizou :
a po co ci to?
zawsze możesz skorzystać ze wzory cos(2x) i to sobie wyliczyć
21 mar 15:56
Mila:
cos(4x)=cos2(2x)−sin2(2x)
21 mar 15:58
Saizou :
tylko ciekawe co chce obliczyć
Damian, bo jak równanie typu cos(4x)=1 to po co to rozbijać

21 mar 15:59
Damian: dzięki, chyba muszę to tak rozbić:
I 2cos4x I > 1
21 mar 16:17
Damian: Pytanie do Mila:
w tej zamianie to robię to tak że przykładowo za 2x podstawiam t czyli 2x=t i liczę to tak jak
dla kąta podwójnego czyli cos2t > 1 i
21 mar 16:19
Mila:
Jeśli masz taką nierówność, to nie trzeba żadnych przekształceń.
2cos(4x)>1 lub 2cos(4x)<−1 i to rozwiązujesz.
21 mar 16:19
Mila:
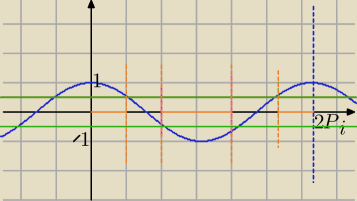
| | 1 | | 1 | |
⇔cos(4x)> |
| lub cos(4x)<− |
| |
| | 2 | | 2 | |
| | π | | 5π | | 2π | | 4π | |
0+2kπ<4x< |
| +2kπ lub |
| +2kπ<4x<2π+2kπ lub |
| +2kπ<4x< |
| +2kπ ⇔ |
| | 3 | | 3 | | 3 | | 3 | |
| 2kπ | | π | | 2kπ | | 5π | | 2kπ | | 2π | | 2kπ | |
| <x< |
| + |
| lub |
| + |
| <x< |
| + |
| |
| 4 | | 12 | | 4 | | 12 | | 4 | | 4 | | 4 | |
| | 2π | | 2kπ | | π | | 2kπ | |
lub |
| + |
| <x< |
| + |
| |
| | 12 | | 4 | | 3 | | 4 | |
21 mar 17:22

