wtf
nicocacola: Dany jest punkt A(−2;5) oraz prosta k: x−2y+2=0 . Oblicz współrzędne pozostałych wierzchołków
kwadratu ABCD wiedząc że przekątna BD zawiera sie w prostej k
20 mar 23:29
nicocacola: błagam pomocy
20 mar 23:29
nicocacola: to jest maturalne z arkusza za 5pkt więc masakra ..
20 mar 23:36
dobra rada:
@Paulina ..... licz swoje zadania !
20 mar 23:37
Paulina:
Musisz być złośliwa ? Policzyłam i czekam na dalsze wskazówki ? Nie zauważyłaś ?
20 mar 23:39
nicocacola: pomoze ktoś ?
21 mar 13:35
wredulus_pospolitus:
krok 1) wyznacz prostą prostopadłą (nazwijmy ją 'l') do prostej 'k', przechodzą przez punkt A
krok 2) oblicz odległość punktu A od prostej k −−− jest to połowa przekątnej kwadratu
krok 3) wyznacz punkt (nazwijmy go O) przecięcia się prostych 'l' i 'k'
krok 4) 'odłóż' wyliczoną odległość z kroku (2) na tych prostych od punktu O
krok 5) i właśnie wyznaczone zostały wierzchołki tegoż kwadratu ... KOOONIEC
21 mar 13:50
wredulus_pospolitus:
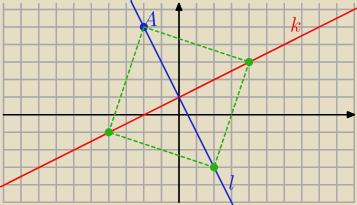
21 mar 14:09
nicocacola: dziękuje

21 mar 14:17
mateusz: mam to samo zadanie w arkuszu

ale nie wiem jak to zapisać rachunkowo
21 mar 19:50
mateusz: czy ktoś by mógł to rozpisać ?
21 mar 19:57
mietek: dostałeś gotowy schemat rozwiązania...
w czym problem?
21 mar 20:00
mateusz: jak to wszystko zapisać..
21 mar 20:11
Mila:
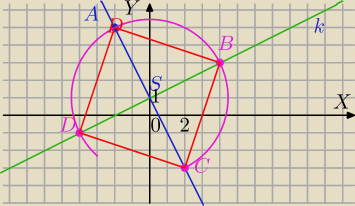
Dany jest punkt A(−2;5) oraz prosta k: x−2y+2=0 .
k:
2) Prostopadła do k i przechodząca przez punkt A
m: y=−2x+b, 5=−2*(−2)+b, b=1
m: y=−2x+1
S− punkt przecięcia przekątnych wyznaczamy jako punkt ptzecięcia prostych m i k
y=1
S=(0,1) − punkt ten jest środkiem symetrii AC i BD
C=(2,−3)
|AS|=
√22+42=
√20
B=(x,(1/2)x+1)
| | 1 | |
|SB|=|SD|=√20=√(x−0)2+( |
| x+1−1)2 |
| | 2 | |
stąd x=4 lub x=−4
Mamy punkty:
B(4,3) i B(−4,−1)
21 mar 20:46


 ale nie wiem jak to zapisać rachunkowo
ale nie wiem jak to zapisać rachunkowo
 Dany jest punkt A(−2;5) oraz prosta k: x−2y+2=0 .
k:
Dany jest punkt A(−2;5) oraz prosta k: x−2y+2=0 .
k: