Perspektywa ktosik: Witam forumowiczów. Przyjmijmy, że mam pewne zdjęcie na którym mogę zobaczyć dom (x− wysokość domu, y − odległość od fotografa). Widzę jednak za domem również na zdjęciu wieżowiec (mniejszy oczywiście niż w rzeczywistości, tzn. z bliska) − jego wysokość to a. Mając te dane chcę obliczyć odległość (oznaczenie: b) wieżowca od fotografa, aby stosunki i dane na zdjęciu były prawdziwe... Myślałem o Talesie, ale sam już nie wiem i się zagmatwałem. Dzięki z góry

Maslanek: Tak jest. Tylko zastanawiam się, czy chcesz to zrobić realnie czy na potrzeby zadania Jeżeli realnie, to musiałbyś pomniejszyć 'x' i 'a' o wysokość Twoich oczu nad ziemią w chwili patrzenia,

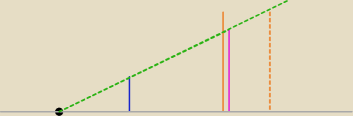
ktosik: Bardziej realnie, choć nie do końca . Załóżmy, że fotograf leżał na ziemi. Szara kropka to fotograf. Niebieska linia to dom. Żeby obliczyć wysokość wieżowca to jego wysokość musiałaby być równa różowej kresce, a jeśli jest równa to pomarańczowej to muszę "przesunąć" trochę tak(przesunięta − pomarańczowa przerywana). No a ten wieżowiec nie mógłby być na tym rysunku pomarańczową ciągłą? Hmm.. No bo nie mam pewności, że "z" wysokości wieżowca oraz wysokości domu i odległości od fotografa "da się utworzyć" tw. talesa..

Maslanek: Hmm... Tzn. chcemy połączyć prostą fotografa, szczyt domu i szczyt wieżowca, ale nie możemy tego zrobić, bo jeśli połączymy szczyt domu i fotografa, to szczyt wiezówca jest nad prostą. Dokonujemy przesunięcia równoległego szczytu o pewną wartość x. Wtedy z twierdzenia Talesa policzylibysmy L+x, gdzie L− odległość wieżowca od fotografa. Więc teoretycznie, jeśli znalibyśmy wartość x to nic nie stoi na przeszkodzie. Przynajmniej wg mnie Jeśli nie znamy, to trochę kicha A nie chce mi się myśleć nad czymś więcej

ktosik: Ok, dzięki