br
Radek:
Podstawą ostrosłupa ABCS jest trójkąt równoboczny ABC o boku długości 8. Punkt D jest
środkiem krawędzi AB , odcinek DS jest wysokością ostrosłupa. Krawędzie AS i BS mają
długość 7. Oblicz długość krawędzi CS tego ostrosłupa.
Mogę prosić tylko o rysunek do zadania
19 mar 20:57
Mila:
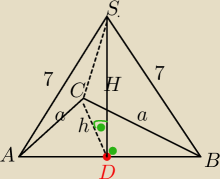
19 mar 21:02
...:
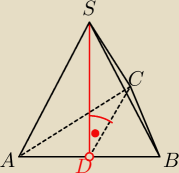
19 mar 21:04
Radek:
z pitagorasa
H2=72−42
H=√33
h=4√3
|CS|2=(4√3)2+(√33)2
|CS|=9 ?
19 mar 21:07
Mila: 
19 mar 21:08
Radek:
Podstawą ostrosłupa ABCD jest trójkąt ABC . Krawędź AD jest wysokością ostrosłupa
Oblicz objętość ostrosłupa ABCD , jeśli wiadomo, że |BC | = 8, |BD | = |CD | = 14 oraz pole
podstawy jest równe 24
Co tutaj najpierw wyliczyć
19 mar 21:14
Marcin: BCD, to trójkąt równoramienny
Wylicz jego wysokość. Wylicz też wysokość trójkąt w podstawie.
19 mar 21:19
Radek:
Z tego mówisz żeby zrobić ? Ok już działam
19 mar 21:22
Marcin: Działaj i podaj wynik. Zobaczę czy wyszło nam tyle samo
19 mar 21:24
Mila:
NNNNNp. tak.
1) wysokość ΔBCD
2) zastanów się jakim Δ jest ΔABC i oblicz jego wysokość
3) AD
Można inaczej.
19 mar 21:24
Radek:
ΔBCD jest równoramienny
19 mar 21:30
Mila:
Pytałam o ΔABC.
To rozwiązuj .
19 mar 21:33
Radek:
równoboczny
19 mar 21:35
Mila:
Dlaczego?
19 mar 21:37
Radek:
AD=2√33 ?
19 mar 21:37
Radek:
To moje pomyłka, o o trójkącie ΔABC nie wiem nic. I AD też źle
19 mar 21:38
Marcin: Ja mam inne AD. Jak to liczysz?
19 mar 21:39
Radek:
AD=12
V=96
19 mar 21:46
Marcin: Tak jak u mnie
19 mar 21:46