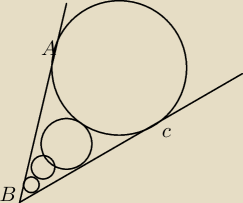
Ciąg geometryczny Blue: Cztery okegi położone są od najmniejszego do największego.Wykaż, że jeśli kąt ABC = 60 stopni i |AB|= 2 √3 cm, to suma długości tych okręgów jest większa od 18,6 cm. Oblicz sumę pól mół ograniczonych tymi okręgami. Doszłam do tego, że promień największego okręgu wynosi 2, ale nie wiem, co zrobić dalej... Jak wyliczyć q? Pomoże ktoś?

Blue: Ps rysunek trochę niewyraźny i źle zrobiony, ale mam nadzieję, że wiecie o co chodzi , te okręgi są styczne do odcinków AB i BC

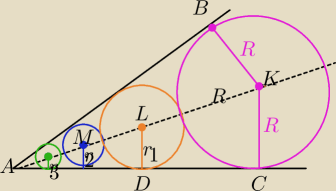Mila: Środki okręgów wpisanych w kąt leżą na dwusiecznej kąta. Okręgi są figurami podobnymi. |AB|=|AC|=2√3cm − punkty styczności okręgu są jednakowo odległe od wierzchołka kąta.

	R		√3		R
tg30o=		⇔		=		⇔R=2cm
	|AC|		3		2√3

Obliczamy promienie r₁,r₂ |AK|=2R=4 (masz Δ ekierkowy : 30,60,90) ΔADL∼ΔACK AL=2r₁

AL		AK		2r1		2r1+r1+2
	=		⇔		=		stąd
r1		R		r1		2

	2
r1=
	3

Analogicznie obliczymy r₂

	2
r2=
	9

Badamy ilorazy:

r1		2		1
	=		:2=
R		3		3

r2		2		2
	=		:		⇔
r1		9		3

R,r₁, r₂,r₃ − kolejne wyrazy c. geom. Dalej liczysz sumę obwodów i pól na piechotę, albo korzystasz własności figur podobnych i c. g. sprawdź rachunki.