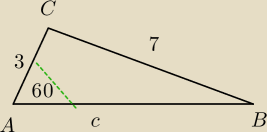
Ostrosłup o podstawie trójkąta jakubs: Podstawa ostrosłupa jest trójkąt ABC w którym. |AC|=3 |BC|=7 |∡A|=60 Oblicz objętość tego ostrosłupa, jeśli wiadomo, że każda krawędź boczna ma długość

	25√3
		.
	3

Spodek wysokości będzie środkiem okręgu opisanego na podstawie, ale nie wiem jak to dalej ruszyć. Jakaś wskazówka ?

bezendu: To wylicz ten promień i potem z Tw Pitagorasa wyliczysz H, pole podstawy chyba wiesz jak ?

jakubs: Zaćmienia dostałem, zapomniałem o Tw. Snelliusa. Dzięki

bezendu: Nie znam tego twierdzenia ?

jakubs: Snelliusa inna nazwa twierdzenia sinusów.

bezendu: To to mi się skojarzyło z odbiciem światła

Janek191: Mamy 7² = 3² + c² − 2*3 c*cos 60^o 49 = 9 + c² − 6 c*0,5 c² − 3 c − 40 = 0 Δ = 9 − 4*1*(−40) = 169 √Δ = 13

	3 + 13
c =		= 8
	2

	√3
Pp = 0,5 *3*8*sin 60o = 12*		= 6 √3
	2

Korzystamy z wzoru:

	a*b*c		a*b*c
P =		⇒ R =
	4 R		4 P

	7*3*8		168		7		7
R =		=		=		=		√3
	4* 6√3		24√3		√3		3

Dokończ

jakubs: Tak tak, ale to jest prawo załamania światła Snelliusa. Między prawem a twierdzeniem są chyba jakieś różnice

jakubs: Janek dzięki za fatygę. Już obliczyłem V=14[j³]