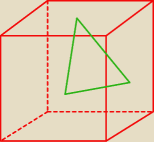
bt Radek: W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta. Tak wygląda rysunek do zadania ?

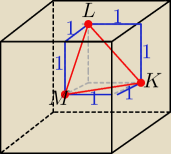
Mila: Tu musisz sobie wyobrazić, że wyjmujesz jeden sześcianik.

Radek: to jest równoboczny o boku √2

	√3
P=
	2

Myśli Pani że zdążę zrobić te bryły i analityczną do maja ?

Mila: Zdążysz na pewno. Przecież w szkole też Cię uczą.

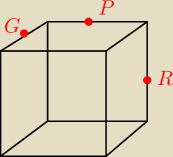
Radek: Narysuj przekrój równoległościanu płaszczyzną PQR . to będzie trójkąt?

Mila: Nie. Poczekaj PW to pięknie tłumaczył, może zaglądnie, jeśli nie to ja narysuję.

Radek: Dobrze, poczekam bo z tymi przekrojami mam trochę kłopot, ogólnie zrobiłem 86 zadań z brył ale jeszcze mam 200 i chcę zrobić to do końca marca no i jeszcze analityczna.

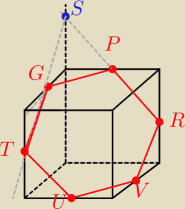
Mila: 1)GP 2)PR, przedłużamy i mamy punkt S 3)SG⇒T 4)TU||PR 5) UV||GP 6)VR Otrzymaliśmy sześciokąt.

Radek: a czemu przedłużamy ?

Mila: Aby wykonać cięcie.Wszystkie punkty muszą znaleźć się w jednej płaszczyźnie.

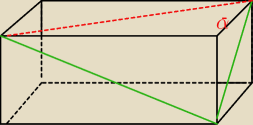
Radek: W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 60∘ , oblicz pole powierzchni tego prostopadłościanu. Czy α ma 90⁰ ?

Mila: Pomyśl, między zielonymi jest kąt 60, obie przekątne równe, czy może tam być kąt prosty?

Radek: nie może

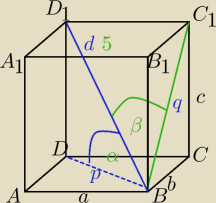
Radek: Przekątna prostopadłościanu ma długość 5 i tworzy z dwoma ścianami prostopadłościanu kąty α i

	3√2		4
β takie, że cosα=		cosβ=		. Oblicz objętość tego prostopadłościanu.
	5		5

Nie wiem jak tutaj z rysunkiem

Mila: To jaki tam jest Δ? 22:23?

Radek: 48. Jeśli wstawiam nowe zadanie to zrozumiałem

Mila:

Radek: Dziękuję za rysunek zaraz postaram się cos policzyć

Radek: wyliczyłem tak:

p		3√2
	=
5		5

p=3√2 |DD₁|=√7 i szukam kąta prostego w ΔBD₁C₁ ale tam go chyba nie ma ?

Mila: Dobre obliczenia. ∡D₁C₁B=90^o D₁C₁ jest prostopadła do ściany BCC₁B₁ to jest też prostopadła do C₁B

Radek: Takich zależności to ja nie znam.

Mila: Przewróć bryłę na ścianę BCC1B1 Jeżeli prosta przebija płaszczyznę i jest do niej prostopdała , to jest prostopadła do każdej prostej leżącej w tej płaszczyźnie i przechodzącej przez punkt przebicia.

Radek: postaram się zapamiętać to twierdzenie bo nie wiem jeszcze kiedy mamy kąt prosty w bryłach

Radek: Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz objętość naczynia. Przyjmując π ≈ 3,14 , wynik podaj z dokładnością do 1 cm 3 . H=8 ale ile jest r ?

Marcin: Kula = jakby 1cm wysokości tego walca

	4
πr2*1=		π27
	3

	4
r2=		*27
	3

r²=36 r=6

Radek: a czemu nie 3 ?

Marcin: Ale skąd 3? Jeżeli wkładasz tą kulę do tego naczynia, to poziom wznosi się o 1cm, czyli Objętość tego walca dla h=1 = objętość tej kuli.

Radek: objętość kuli ?

Marcin: Objętość tego walca dla wysokości 1cm wyniesie πr², musisz teraz zauważyć, że o 1 cm podnosi się woda po włożeniu kuli. Wieć objętość tej kuli= co?

Radek: no właśnie objętość kuli to co ?

Marcin:

4
	πr3 − r przecież znasz.
3

Radek: no tak ale to równa się czemu ?

Marcin: To się równa objętości tego walca dla wysokości równej 1cm. Jeżeli masz 7 litrów wody w wiadrze, i po nalaniu tam z butelki wody robi się nagle 8l, to objętość tej butelki będzie równa 1l z tego wiadra, rozumiesz?

Radek: teraz tak

Marcin: