jak wygląda twierdzenie odwrotne do Twierdzenia Talesa ? as: jak wygląda twierdzenie odwrotne do Twierdzenia Talesa ?

PW: Jak każde twierdzenie odwrotne. Twierdzenie odwrotne do p ⇒ q ma postać q ⇒ p.

Mila: http://www.math.edu.pl/twierdzenie-talesa

daras: wujek Google nie pomógł ?

as: to twierdzenie odwrotne wyglada tak samo jak twierdzenie talesa ? Bo nie widze roznic

PW: A widzisz różnicę między zdaniem "jeżeli liczba n∊N dzieli się przez 4, to n dzieli się przez 2" a zdaniem "jeżeli liczba n∊N dzieli się przez 2, to n dzieli się przez 4"? To jest przykład twierdzenia i twierdzenia do niego odwrotnego.

as: dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M,N są odpowiednio środkami boków AB i CD. Punkty P,Q są odpowiednio środkami przekątnych AC i BD. Uzasadnij, że MQllPN. Korzystając z twierdzenia odwrotnego do twierdzenia Talesa:

|DN|		|NC|
	=
|AP|		|PC|

to jak wygląda w tym przypadku normalne twierdzenie Talesa ?

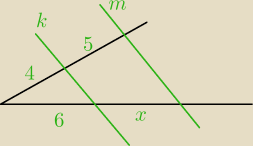
Mila: zał. k||m oblicz długość odcinka x. Z tw. Talesa

4		5
	=		i obliczasz
6		x

as: a odwrotne do Tw talesa to:

6
	= x5 ?
4

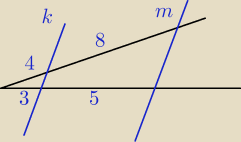
Mila: Sprawdź czy proste k i m są równoległe. Z tw. odwrotnego do tw. Talesa

4		8
	=?
3		5

4*5=?8*3 20≠24 odcinki wyznaczone na ramionach kąta nie są proporcjonalne, zatem proste k, m nie są rownoległe.

PW: Zacytuję: Korzystając z twierdzenia odwrotnego do twierdzenia Talesa:

|DN|		|NC|
	=		...
|AP|		|PC|

I co dalej? Czemu nie korzystasz z tego twierdzenia − nie wyciągasz wniosku o równoległości, tylko uprawiasz jakąś galopadę myślową kończąc to pytaniem o twierdzenie Talesa? W tym zadaniu twierdzenia Talesa nie zastosujesz, bo nie wiesz nic o żadnych prostych równoległych.

as: ja mam tak zadanie rozwiązane i napisane że jest to twierdzenie odwrotne do tw. Talesa

as: ja wiem co dalej zrobić tylko nie rozumiem o co chodzi z tym twierdzeniem odwrotnym do twierdzenia talesa jak je się wyznacza

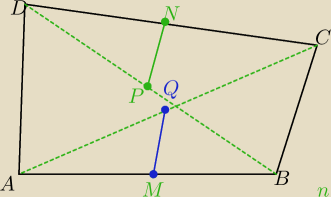
Mila: DN=NC z założenia PD=PB z założenia

	DN		PD
⇔		=		=1⇔NP||BC
	NC		PB

(Na ramionach kąta CDB zostały wyznaczone odcinki proporcjonalne przez proste NP i BC) Analogicznie :

AQ		AM
	=		⇔MQ||BC
QC		MB

(Na ramionach kąta CAB zostały wyznaczone odcinki proporcjonalne przez proste MQ i BC) Zatem: NP||BC i MQ||BC ⇔NP||MQ