 Cześć mam jutro sprawdzian i zadano nam kilka zadań, które muszę rozwiązać, pomoże ktoś?
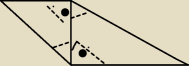
1. DC=AC=a oraz AB= √3. Przekątna AC tworzy z bokiem AD kąt ostryα, zaś z bokiem CB kąt
ostryβ oraz AC jest prostopadły odo DC i AC prostopadły do AB.Wobec tego sinα+cosβ ma wartość?
a] {3}/2 + 1 b] 2 + {2} /2 c] {2}/2 + {3}/2 d] √2 +1 / 2
ten w lewym trójkącie na dole to jest α, a u góry w prawym trójkącie β
2. Wiadomo, że α należy (90, 180 stopni) oraz sin(90+α) − 3cosα=1
Zatem tngα = ?
3.Wiadomo, że α= loga2sin45 stopn. WObec tego α należy:
a] α należy (−1,0) b] α należy (− nieskończoność,−1) c] α należy (0,1) d] α
należy (−1,1)
4. Wykaż, że jeśli sin α * cos α = 0,3 i α jest kątem ostrym to
Cześć mam jutro sprawdzian i zadano nam kilka zadań, które muszę rozwiązać, pomoże ktoś?
1. DC=AC=a oraz AB= √3. Przekątna AC tworzy z bokiem AD kąt ostryα, zaś z bokiem CB kąt
ostryβ oraz AC jest prostopadły odo DC i AC prostopadły do AB.Wobec tego sinα+cosβ ma wartość?
a] {3}/2 + 1 b] 2 + {2} /2 c] {2}/2 + {3}/2 d] √2 +1 / 2
ten w lewym trójkącie na dole to jest α, a u góry w prawym trójkącie β
2. Wiadomo, że α należy (90, 180 stopni) oraz sin(90+α) − 3cosα=1
Zatem tngα = ?
3.Wiadomo, że α= loga2sin45 stopn. WObec tego α należy:
a] α należy (−1,0) b] α należy (− nieskończoność,−1) c] α należy (0,1) d] α
należy (−1,1)
4. Wykaż, że jeśli sin α * cos α = 0,3 i α jest kątem ostrym to
| 1 | 1 | |||
(tgα + | )2= 11 | |||
| tgα | 9 |
| sinα | sinα | 2 | ||||
− | = − | |||||
| cosα−1 | cosα+1 | sinα |
| sinα | sinα | |||
6. Oblicz wartość wyrażenia | − | , dla α=150 stopni | ||
| cosα−1 | cosα+1 |
| 1 | 1 | cosα+1 − (cosα −1) | ||||
sinα ( | − | = sinα( | = | |||
| cosα − 1 | cosα +1 | (cosα−1)(cosα+1) |
| 2 | 2 | 2 | ||||
sinα | = sinα | = − | , | |||
| cos2α − 12 | −sin2α | sinα |
| 2 | ||
− | . | |
| sin150° |