 Czy może ktoś mi wyjaśnić, gdzie robię błąd w tym rozwiązaniu.
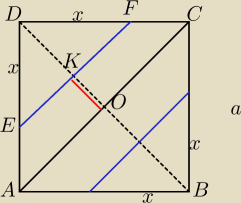
"w kwadracie, którego bok ma długość a, poprowadzono proste równoległe do jednej z przekątnych
w równych od niej odległościach. Podzieliły one ten kwadrat na trzy części o równych polach.
Oblicz odległość tych prostych od przekątnej kwadratu."
Czy może ktoś mi wyjaśnić, gdzie robię błąd w tym rozwiązaniu.
"w kwadracie, którego bok ma długość a, poprowadzono proste równoległe do jednej z przekątnych
w równych od niej odległościach. Podzieliły one ten kwadrat na trzy części o równych polach.
Oblicz odległość tych prostych od przekątnej kwadratu."
| a2 | ||
Pole trójkąta DAC = | ||
| 2 |
| a2 | ||
Pole trójkąta DEF to | , bo każde z pól jest takie same, a pola są 3. | |
| 3 |
| 2 | √6 | |||||||||||||
skala k2= | = | zatem k= | |||||||||||||
| 3 | 3 |
| a√2 | √6 | a√2 | a√3 | |||||
IODI = | IDKI = | * | = | |||||
| 2 | 3 | 2 | 3 |
| a√2 | a√3 | 3a√2 − 2a√3 | ||||
IOKI = | − | = | ||||
| 2 | 3 | 6 |
| a(√3 − √2)√6 | ||
Prawidłowy wynik to | ||
| 6 |
| 3a√2−2a√3 | a√9*2−a√4*3 | |||
|OK|= | = | = | ||
| 6 | 6 |
| a√3*6−a√2*6 | a√6(√3−√2) | a(√3−√2)√6 | ||||
= | = | = | .  | |||
| 6 | 6 | 6 |
