Wredna koza. pie: W narożniku trawnika o wymiarach 3 m na 7 m wbito kołek, do którego przywiązano na sznurku żarłoczną kozę. Wykaż, że długość x sznurka pozwalająca kozie na zjedzenie trawy z dokładnie z połowy trawnika spełnia warunek 2√3 < x < 3√2. Coś z własności funkcji ciągłych.

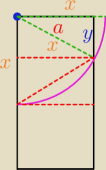
Maslanek: P=3*7=21

	21
Czyli koza ma zjeść z		m2 trawnika.
	2

	m
P{wycinka)=		*r2, gdzie m−kąt w radianach
	2

	y		x2−9		x2−9
Mamy; sina=		, gdzie y=x2−32, czyli sina=		⇒ a=arcsin
	x		x		x

	π		a		1
Tutaj pole: P=		x2−		x2+		*3*x*sina
	4		2		2

Nie wiem czy wyjdzie co trzeba

Maslanek: Może gdyby wziąć:

	π		a		3		21
Pewną funkcję P(x)=		x2−		x2+		x*sina−		i policzyć jej pochodną, to
	4		2		2		2

P'(x)=0 lda x∊(2√3, 3√2). Oczywiście a zastępujemy przez wyrażenie z x

pie: Chyba ogarnę. Pochodnej nie trzeba liczyć, wystarczy P(2√3) i P(3√2).

Maslanek: Trzeba . Pochodna wskaże co się dzieje między tymi dwoma punktami. Zaś wartość w dowolnym punkcie w przedziale pokaże jaka jest wartość na całym przedziale.

pie: Mój podręcznik twierdzi, że mam to zrobić z twierdzenia o przyjmowaniu wartości pośrednich, bo pochodne w następnych tematach. Przynajmniej tak jest w odpowiedziach.