objętość i pole powierzchni bocznej ostrosłupa czworokątnego
alicja1995: podstawą ostrosłupa czworokątnego jest romb o przekątnych długości 6 cm i 8 cm, a punkt
przecięcia przekątnych podstaw jest spodkiem wysokości. krawędź boczna tego ostrosłupa jest
nachylona do płaszczyzny podstawy pod kątem 45 stopni. oblicz:
a) objętość ostrosłupa
b) pole powierzchni bocznej ostrosłupa
c) pole przekroju zawierającego dłuższą przekątną podstawy i wierzchołek ostrosłupa
17 mar 18:09
ghj:
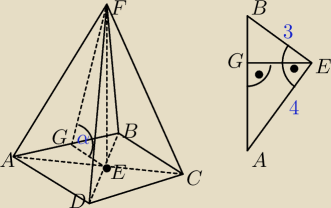
α = 45
o; |AC| = 8 cm; |BD| = 6 cm;
W ΔABE
|AB| = 5 cm (Pitagoras)
P
ΔABE =
12 * |AE| * |BE| =
12 * |AB| * |GE|
|AE| * |BE| = |AB| * |GE|
4 * 3 = 5 * |GE|
|GE| = 2,4
ΔGEF to trójkąt prostokątny równoramienny (patrz kąty), czyli:
|GE| = |EF| = 2,4 (wysokość ostrosłupa)
|GF| z tw. Pitagorasa można obliczyć i już możesz wszystko policzyć
W podpunkcie c) przekrojem będzie ΔACF
17 mar 18:50
walt: Czy to aby na pewno jest ok?

17 mar 19:00
anonim: a nie źle, ja przeczytałem ściana boczna jest nachylona do płaszczyzny podstawy a powinna być
krawędź boczna. Czyli rysunek i obliczenia ŹLE
17 mar 19:02
 α = 45o; |AC| = 8 cm; |BD| = 6 cm;
W ΔABE
|AB| = 5 cm (Pitagoras)
PΔABE = 12 * |AE| * |BE| = 12 * |AB| * |GE|
|AE| * |BE| = |AB| * |GE|
4 * 3 = 5 * |GE|
|GE| = 2,4
ΔGEF to trójkąt prostokątny równoramienny (patrz kąty), czyli:
|GE| = |EF| = 2,4 (wysokość ostrosłupa)
|GF| z tw. Pitagorasa można obliczyć i już możesz wszystko policzyć
W podpunkcie c) przekrojem będzie ΔACF
α = 45o; |AC| = 8 cm; |BD| = 6 cm;
W ΔABE
|AB| = 5 cm (Pitagoras)
PΔABE = 12 * |AE| * |BE| = 12 * |AB| * |GE|
|AE| * |BE| = |AB| * |GE|
4 * 3 = 5 * |GE|
|GE| = 2,4
ΔGEF to trójkąt prostokątny równoramienny (patrz kąty), czyli:
|GE| = |EF| = 2,4 (wysokość ostrosłupa)
|GF| z tw. Pitagorasa można obliczyć i już możesz wszystko policzyć
W podpunkcie c) przekrojem będzie ΔACF
